Continuing on in our review of basic math, I welcome you to Day 2. The answers to Day 1 questions are at the bottom of the post — along with new questions. But first, let’s learn how to multiply and divide integers.
Let’s say you have a bank account with a service fee of $15 per month. If that amount was deducted every single month, how can you represent the yearly amount for these fees? Well, you would multiply -$15 (the fee is negative because it’s taken out of the account) by 12 (the number of months in the year). But how the heck do you multiply negative and positive numbers? Let’s find out.
Remember integers — those negative and positive numbers that aren’t fractions, decimals, square roots, etc.? I like to think of them as positive and negative whole numbers (though most real mathematicians would argue against that classification). On Wednesday, you learned how to add and subtract these little buggers. (Check out the post here, if you missed it.) Today, we multiply and divide.
Her’s the really good news: it is way, way easier to multiply and divide integers than to add and subtract them. First, though, it’s a good idea to understand how the rules work. When you first started multiplying numbers, you did things like this:
2 x 3 = 2 + 2 + 2 = 6
In other words “2 x 3” is the same thing as adding up three 2s. Get it? And because you started working with positive numbers when smacking a girl upside the head meant you “like-liked” her, you know without a shadow of a doubt that the answer is positive.
Let’s see what happens when you multiply a negative number by a positive number:
-2 x 3 = -2 + -2 + -2 = -6
Now to understand this, you need to either pull up your mental number line and count or remember the addition rules from Wednesday’s post. When you add two numbers with the same sign, add the numerals and then take the sign. So -3 + -3 is -6.
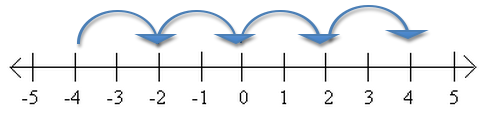
But what about multiplying two negative numbers? Admittedly, this is a little trickier to explain. It helps to look for a pattern using a number line. Let’s try it with -2 x -3.
-2 x 2 = -4
-2 x 1 = -2
-2 x 0 = 0
-2 x -1 = ?
-2 x -2 = ?
Based on the pattern shown on the number line, what is -2 x -1? What is -2 x -2? If you said 2 and 4, you are right on the money.
And now we can summarize the above with some rules. Believe me, this is one math concept that is much, much easier to remember with the rules. Still, if knowing why helps anyone get it, I’m all for pulling back the curtain.
When multiplying integers:
If the signs are the same, the answer is positive;
If the signs are different, the answer is negative.
Bonus: The same rules work for division. That’s because division is the inverse (or opposite) of multiplication.
When dividing integers:
If the signs are the same, the answer is positive;
If the signs are different, the answer is negative.
The only tricky part is this: Sometimes it seems that if you are multiplying or dividing two negative numbers, the answer should be negative. It’s a trap! (Not really, but you could think of it that way, if it helps.) The key in multiplying and dividing integers is noticing whether the signs are the same or different.
In fact, if you are doing a whole set of these kinds of problems, you can simply run through the problems and assign the signs to the answers — before even multiplying or dividing. (I tell students to do this all the time, because I think it helps them to remember the rules.)
4 x -3 → signs are different → answer is negative
-4 x -3 → signs are the same → answer is positive
-4 x 3 → signs are different → answer is negative
4 x 3 → signs are the same → answer is positive
Then all you’d need to do is the multiplication itself:
4 x -3 = -12
-4 x -3 = 12
-4 x 3 = -12
4 x 3 = 12
And like I said, division works the same way:
-24 ÷ -2 = +? = 12
24 ÷ -2 = -? = -12
24 ÷ 2 = +? = 12
-24 ÷ 2 = -? = -12
Got it? Try these examples on your own.
1. 5 x -6 = ?
2. -18 ÷ 9 = ?
3. -20 ÷ -4 = ?
4. 8 x 4 = ?
5. -2 x 7 = ?
Questions? Ask them in the comments section. Up Monday are fractions. If you can’t remember how to add, subtract, multiply or divide fractions or mixed numbers, tune in.
Answers to Wednesday’s “homework.” (It’s not really homework, I promise.) -10, -4, 2, -15, -2. How did you do?