So yesterday, we reviewed some really basic stuff about percentages. Like: 10% is the same thing as 1/10 or 0.1. Easy peasy, right? Well, today it’s time to really put this stuff to work, finding percentages of numbers or the numbers, given the percentages. Oy. I can hear you groaning from here.
Most folks forget when to multiply and when to divide. So I’m going to show you a process that works no matter what kind of percentage problem you’re doing. For reals. It’s why it was important for you to know about turning percentages into fractions. Let’s start with an example.
You’ve had your eye on a gorgeous cashmere sweater for months and it’s finally on sale. But can you afford it? The original price is $125, but it’s now on sale for 30% off. Do you multiply or divide or what to find out what you’d be saving with this sale?
All you need for this problem — and pretty much all other percentage problems — is to set up a proportion. What is that, you ask? A proportion is made up of two equal ratios or fractions. The proportion you need for a percentage problem is this one:
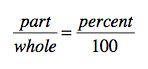
If you can remember this proportion — and how to use it — you’re home free. So let’s dissect it a bit to help you remember. The fraction (or ratio) on the right of the proportion represents the percentage itself. You should recognize this from yesterday, when you learned to change a percent to a fraction, right? So in this problem, that ratio will be 30 over 100. That’s because the sweater is 30% off.
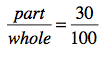
The ratio on the left is a little tricker, but not by much. It is the percent off of the sweater over the original price of the sweater: the part of the price over the whole price. Got it? The original price (or whole price) is $125. But we don’t know the discount (or part of the price). Let’s call that x.
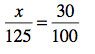
DON’T PANIC! That little old x isn’t going to hurt you one bit. Promise. Just because you have an x in your math problem does not make it too challenging to solve.
But yes, you will need to solve for x. This involves two, very simple steps: Cross multiply and then get x by itself. There are tons and tons of shortcuts for this kind of a problem, but for now, we’re going to stick with the more scenic route.
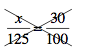
To cross multiply, just multiply the x by 100 and then the 125 by the 30.
100x = 125 • 30Do you have to have the equation in that order? Nope. 125 • 30 = 100x works the same way. Heck you can even multiply in any order. Now, just start simplifying and getting x by itself:
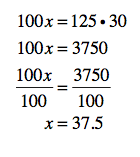
Now, remind me, what is x? Is the price of the sweater? Nope. It’s what you would save if you bought the sweater at 30% off. The sale price of the sweater is $125 – $37.5 or $87.50.
That wasn’t so painful, was it?
But what if you needed to know what percent a number was of another number? Let’s say you just had lunch with your dad, who is known for being a bit stingy. He left a $7.50 tip on a $50 check. Was it enough? Well, set up that proportion, why don’t you?
What’s the whole? $50 or the total cost of lunch. And what’s the part? That would be the tip or $7.50. You are trying to find the percent, and 100 is always 100. Substitute, cross multiply, isolate x and voila!
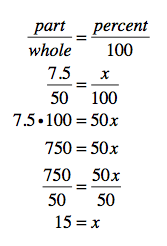
Looky there, good old Dad did okay with the tip — 15%.
You can also use this proportion to find the whole, when you know the percentage and the part. Just substitute what you know, shove xin there for what you want to find and follow the same darned steps as the previous examples.
Seriously ya’ll, if you can remember this one proportion, percentages will no longer be a huge stumbling block. But I can hear a couple of you whining: “What about percent increase or percent decrease???” You’ll have to wait until Friday. (Promise. It’s not all that difficult either.)
This is a good thing to practice, so try out these problems. Remember: Identify the part, whole and percent before you use the proportion. (That’s not going to be as easy with these, because they’re not word problems.) Then cross multiply and get x by itself.
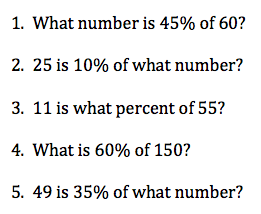
Questions about this process? Do you have any better ideas? (I’ll bet you do!) Share them in the comments section. Meanwhile, here are the answers to yesterday’s percent problems: 11/20, 41/50, 3/20, 0.04, 0.31, 1.4. How did you do?
