My thumb isn’t even remotely green. The only plants I have any success with are those that can sustain a tremendous amount of neglect — like hydrangea, hostas and lariope. So I asked fellow write and founder of Outlaw Garden, Cristina Santiestevan to step in with some gardening math. She does not under-deliver! Check out the mad geometry skills she has. Then put her tips to work in your own garden.
In the garden, math is everywhere. There’s arithmetic and subtraction, which gardeners use to estimate how long it will take for a tomato to ripen or a seed to sprout. There’s multiplication, which helps gardeners calculate expected yields. And, there’s higher math too. Lots and lots of higher math.
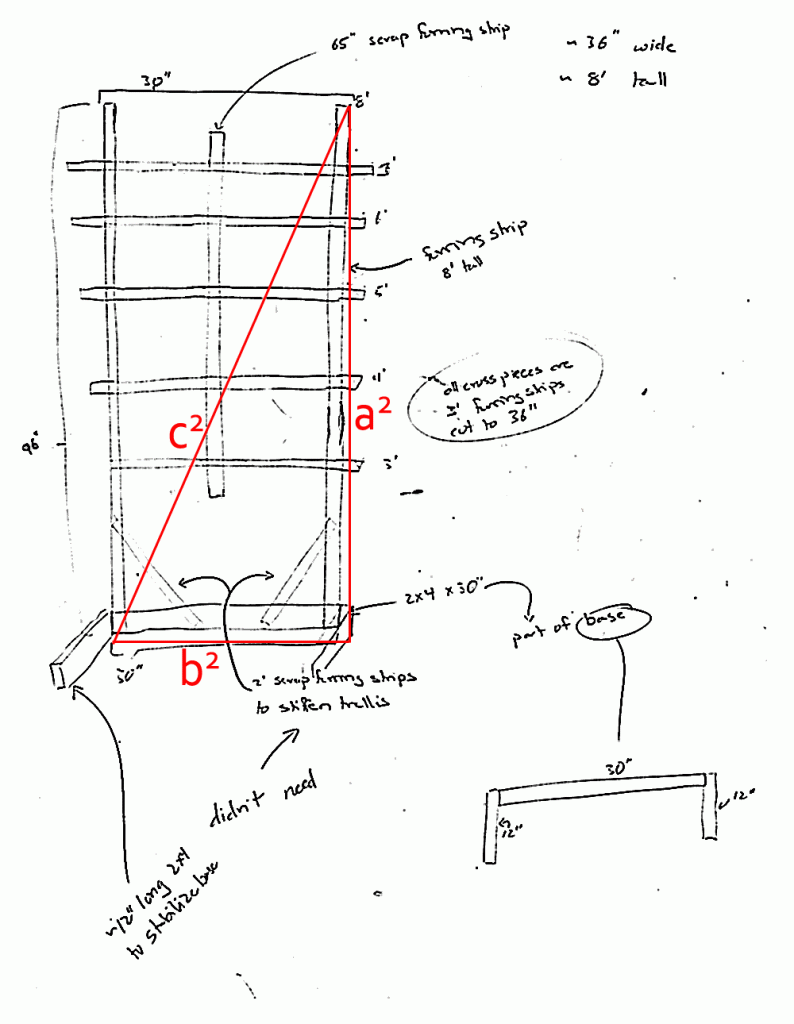
Yesterday, for example, I used a measuring tape and a bit of high school geometry to confirm that my tomato trellis would be a nice (right-angled) rectangle, rather than a slightly askew parallelogram. I also used an online calculator, because figuring out the square root of 10,116 isn’t especially easy to do by hand. I knew I’d get a number close to 100, but I wanted to be sure.
Turns out that the square root of 10,116 is 100.57832768544127. I rounded to 100.5, because my measuring tape isn’t quite that fine-tuned.
If you haven’t guessed yet, I was using the Pythagorean Theorem: a2 + b2 = c2. As an avid DIYer, I use this formula a lot. It’s a great way to be sure that your project will be square, with four right angles. That’s essential if you’re building any sort of box, especially if you’ll be adding a door later. A slight skew away from 90° can create all sorts of trouble.
In this case, the motivation is all aesthetics. This trellis could work fine as a parallelogram. The tomatoes wouldn’t even notice. But, I would.
So, here’s how I did it. The trellis is 96 inches tall and 30 inches wide. Those are our a and b sides. Putting them into the equation, we get 962 + 302 = c2. That works out to
9216 + 900 = c2
10,116 = c2
This is when I googled “square root,” in hopes of finding an online square root calculator. I knew it would come in close to 100, because 100 • 100 = 10,000. But, I wanted to be as exact as possible. That’s where the online calculator came in handy. The answer — 100.57832768544127 — was more precise than I really needed. 100.5 inches is plenty good enough when building trellises in the garden.
With that number in mind, I measured the diagonal from top to bottom on both sides of the trellis. One side measured about 100.25 inches and the other measured about 100.75 inches. A slight adjustment, and both sides measured 100.5 inches. The trellis was square. Success!
Here’s the plan for the trellis. You can see where the right triangle would go:
(Cristina has a great post detailing the step-by-step process for building her trellis, including a downloadable pdf of her plans. Check it out here.)
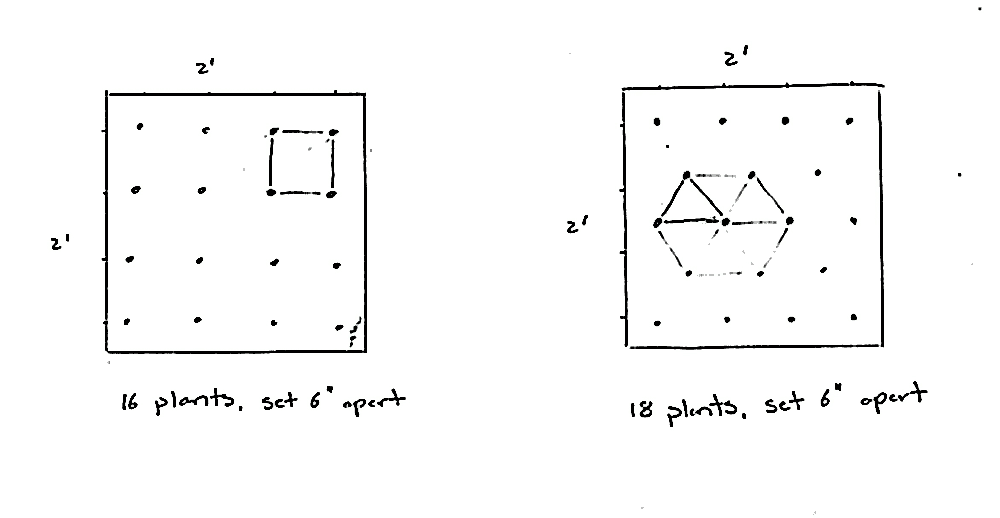
Trellises aren’t the only place we use and see geometry in the garden. The Pythagorean Theorem is a great help to gardeners who want to ensure their garden beds and paths are perfect squares or rectangles, for example. And, equilateral triangles — three equal sides — provide guidance when planting the garden. While most books tell us to plant our vegetables in rows that are square to each other, that’s not the best way to maximize our garden space. No. Instead, plant your rows on a diagonal, using an equilateral triangle as your guide, and you will be able to fit more plants into the same amount of space. Like this:
See how a series of six triangles creates a hexagon in the diagonal planting pattern? That’s where the extra space efficiency comes in; you’re basically planting on a hexagonal pattern. And, as bees already know, the hexagon is the most efficient shape.
Even plants have geometry. All members of the mint family have perfectly square stems, like this bee balm:
Sedges — a grass-like bog plant — have triangular stems. Some plants, like dogwood and maple trees, follow a perfect symmetry with their leaves. These are known as opposite plants, because their leaves form opposite one another on their branches. Alternate plants, on the other hand, form their leaves singularly or in groups, on alternate sides of the branch. Other plants grow their leaves and flowers in whorls or rosettes:

The dogwood has opposite leaves.

Virginia Sweetspire has alternate leaves.

The leaves of the culversroot are in a rosette pattern.
And, the Fibonacci Sequence is everywhere:

The pattern of the yellow spirals in this chamomile are based on the Fibonacci sequence
Thank you, Cristina! My advice to you, dear reader: do not miss her blog, Outlaw Garden; it’s funny, informative and really, really clever. Do you spend time in the garden? What kind of math do you use and see while tending your plants? If you have questions, don’t hesitate to ask in the comments section. Don’t worry, I’ll ask Cristina to come by to respond. (It’ll be better that way.)








Comments are closed.