We’re wrapping up a review of fractions today. If you missed Monday’s or Wednesday’s posts, be sure to look back to refresh your memory on multiplying and dividing fractions.
If you’re the product of a traditional elementary and middle school education, you likely spent many, many months (collectively) learning about adding and subtracting fractions. It is definitely one of the trickiest arithmetic skills to have, but it can also be quite useful. Now that you know how to multiply with fractions, you’re ready to unlock the secret of adding and subtracting them. And it all comes down to multiplying by the lowly, little 1.
This process is really easy — if the fractions in question have one important characteristic. Take a look:
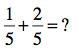
Don’t solve the problem! Just look. What do the fractions have in common? You’re one smart cookie, so I’m sure you recognized that the denominators (the numbers on the bottom of the fractions) are the same — 5. And that’s the key in this process. Whenever you’re adding or subtracting fractions, you need to have common denominators. Then, all you need to do is add the numerators together and keep the same denominator.
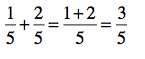
If you took a few moments to run this through your brain, you probably wouldn’t have even needed to know this rule. And since we’re grownups, we can use this example: If you have 1 fifth of Jack Daniels and 2 fifths of Johnny Walker, how many fifths of alcohol do you actually have? Well, that would be 3 bottles or 3 fifths. (And believe me, while some of my high school students would have appreciated that example, I don’t think I could have gotten away with using it.)
Same thing is true for subtraction. Let’s say that the fraternity πππ (yeah, I made that up) is having a huge party. They’ve purchased 7 fifths of bourbon. But just before the gig gets started, one of the brothers knocks over the bar and breaks 3 of the fifths of bourbon bottles. How many are left? Well, that would be 4, right? Using this analogy, you can see that because the denominator was the same (5), all you needed to do was subtract the numerators (7 – 3) to get what was left (4).
And here’s where you can break even more rules. As a grownup, you can do these things in your head. If you need to add 1/8 yards of fabric to 1/8 yard of fabric, it’s pretty simple to see that you’re dealing with 2/8 yard (simplified, that’s 1/4 yard).
Yeah, things get a little trickier when you have different denominators. Let’s go back to that pizza example from Monday, shall we? Remember, we were figuring out how many pizzas to order, if we knew how much each person typically eats. Let’s say that you can eat 1/4 of a pizza, your sister can eat 1/3 and your brother can eat 1/2? In other words:
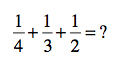
Notice something? Yep — no common denominator. So how do you get one? Well, there’s the short cut and then there’s the longer explanation. In case you’re curious, let’s talk explanation first.
You need a number that all three of these denominators will divide into evenly. That’s called a common multiple. In fact, it’s best if you have the least common multiple. (If you have a really good memory, you might remember that this is often referred to as an LCM.) So what’s the LCM of 4, 3 and 2? Turns out to be 12.
So the common denominator is 12, but do you just replace all of the denominators with a 12, adding 1/12, 1/12 and 1/12? No way, Jose. That won’t get you the right answer. What you need to do is change the numerator so that the denominator is 12. And to do that, you need to multiply by 1.
Remember 1 is the same as any fraction that has the same number in the numerator and denominator. So to change 1/4 to a fraction with 12 in the denominator, you’ll need to multiply by 3/3.
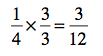
So, think ahead: what do you need to do to turn the other fractions into ones with 12 in the denominators? Multiply by 1. But which 1? You need to think about what number multiplied by the denominator will give you 12.
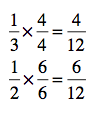
There’s another way to think about this, for sure. Think about the denominator you want: 12. What is one-fourth of 12? 3, right, so 1/4 is the same thing as 3/12. For some folks, that way of thinking is going to work much, much easier. But you can choose what works for you. Now we can solve the problem:
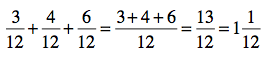
So in this case, you need a little more than one pizza. You can either ask your siblings to eat a little less (and get by on one pizza) or you can order two pizzas and put the rest in the freezer. (Personally, I’d choose the second option.)
Subtraction works the exact same way! Just find the common denominator and change the fractions. Then subtract, and finally, simplify your answer (if necessary).
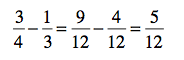
Got it? If not, ask your questions in the comments section. And make sure you try out these practice problems to see how well you can really do! (Remember, no one’s grading anything, so what have you got to lose?)
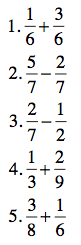
If you have questions, don’t forget to ask them in the comments section. I also love to hear about different ways to approach these ideas. Don’t be afraid to tell us how you do things differently.
Here are the answers to Wednesday’s practice problems: 15/4, 7/16, 28/15, 30, 1/3.
