Ever have one of those strings of bad ju-ju that just won’t quit? Welcome to the last two weeks of my life. From email woes to blog problems, it’s as if the electronic gods have cursed me. This is my way of explaining why there was no post yesterday. I’ll make it up to you today — as I wait on hold for the good folks at Comcast to answer my call about my email account. Wish me luck!
It’s the third week of our review of basic math. Time for percents. These little guys are everywhere — from the mall to your tax return to your kid’s grades to the nutritional label on your Cheerios. You simply cannot go a day without coming across a percent in one form or another.
(Try it. Just for today, notice the percents. If you’re so inclined, jot them down and post what you noticed in the comments section.)
So what’s the big deal? What are percents so darned ubiquitous?
Percents represent a part of the whole. We love to know what part of our extra-cheese, deep-dish pizza is fat or what part of the population is in favor of gun control. This information helps us make decisions and form opinions. And because of the way that percents are found, they’re not so challenging, actually.
First the basics: if you break down the word percent, you will immediately understand what it means. Per means every and (in the U.S.) a cent is 1/100 of a dollar. So percent literally means for every 1/100. Get it? (It should be noted that the notion of a percent came long before the U.S. penny, but the one-cent coin has its roots in Roman currency, which launched percents. Cool, huh?)
With this information, you can easily convert a percent to a fraction — which is a pretty darned useful thing to know. 10% is the same thing as 10 for every 1/100 or 10/100. The only thing left to do is simplify.
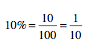
See what I did there? To turn a percent into a decimal, just put the percent over 100 and simplify. Works like a charm every single time.
But what about turning a percent into a decimal? That’s even easier. There are a couple of ways to look at this, but I chose 10% for a good reason. It’s the same thing as 1/10 or if you say it out-loud: “one-tenth.” And what’s another way of writing one-tenth? Put a decimal on it.

Think about what you learned in elementary school about decimals. One place to the left of the decimal point is the “tens” place. One to the right is the “tenths” place. Two places to the right is the “hundredths” place. And so on. If percents mean out of 100 or for every 1/100, really what you’re doing is thinking of place value.
10% = 0.10 = 0.1
All of this boils down to a really simple process. To change a percent to a decimal, move the decimal point two places to the right. Here are some examples:
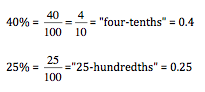
Incredibly basic stuff, right? But it is important. We can use this information to help find the percent of a number or find the value of the whole, given the percent (which is a little bit harder). That’s up tomorrow and Friday.
Until then, how about giving these really simple problems a go?

Any of the above problems give you trouble? (Yep, I snuck in a few toughies, but I know you can do it. Just think it through.) Here are the answers to last Friday’s fraction problems: 2/3, 3/7, -3/14 (Yowza! That was a tricky one!), 5/9, 13/24.
