What’s the most common math question I get from grownups? Easy: What’s the big deal about compound interest? For some reason, this idea stumps some very smart people. But the whole thing is pretty simple really. (Ha!) It all comes down to one concept — curves vs. lines.
You probably know that simple interest is, well, simple. That’s because it’s linear. (Stay with me here. I promise it’s not too hard.) In other words, simple interest can be described as a line. Now in mathematics, lines are very specific things. They go on forever, for one thing. For another, they’re straight. So while I might casually use the word “line” to describe a squiggly while I’m doodling, that’s a huge no-no in math. Among the Pythagorii and Sir Isaac Newtons, there’s no such thing as a “straight line.” By definition, a line is straight, not curved.
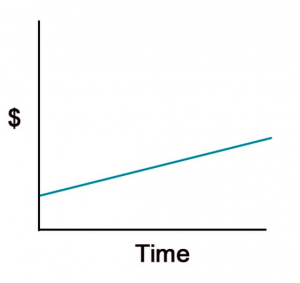
Because simple interest is linear, it increases (and decreases) steadily. Remember graphing linear equations? Take a look:
The graph above is an example of simple interest. As time goes on (or as you look to the right on the “time” axis), the money, $, increases. And it increases very steadily. If you can remember back to your algebra class, you know that each point on this line is found by taking the same steps — x number of “steps” to the right and y number of “steps” up. This is consistent. In other words, you don’t take 2 steps to the right and 1 step up and then 2 steps to the right and 4 steps down. (If you were really paying attention in algebra class, you might remember that this is a way of describing slope, which indicates the steepness of the line.)
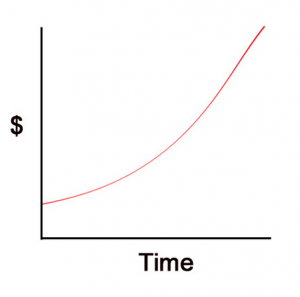
Now curves are different. And, yep, you guessed it, compound interest is a curve. Here’s a general example:
If you looked at three points on this graph, you would find that the way to get from the first to the second to the third is not a consistent series of steps. There would be a pattern, yes, but it wouldn’t be the same each time. This is what we call a non-linear equation, because, well, it’s not linear. (Duh.)
But what can these graphs tell us? It’s not as hard as you might think. Take a look at the graphs themselves. As time increases, so does the money, right? (In other words, as you move to the right along “time” the graph moves up along “$.”) But with the curve, the $ gets bigger faster. It takes less time for the money to increase along the curve than it does along the line. (Follow me? If not, take a closer look at the graphs.)
That’s because of one simple fact: with compound interest, the interest is accrued on the principal (or original amount) and the interest. Each time the interest is calculated, the interest from the previous time period is added to the amount. On the other hand, with simple interest, the interest is accrued on the principal alone. That translates to a steady increase over time, rather than a sharp increase, like with the curve.
So what does this matter? Well, it depends on whether your spending or saving. Since with compound interest, the amount accrues faster over time, this is a good thing for savings or investments — but a bad thing for credit. And it’s the other way around for simple interest.
(Of course that is all moot, since unless you’re borrowing from good old dad, simple interest is pretty hard to come by.)
The point is this: if you can remember that simple interest is a line and compound interest is a curve, you will likely remember how simple and compound interest are figured — slow and steady or speedy quick.
Do you have questions about compound or simple interest? Is there another way that you remember the difference? Share your ideas in the comments section.







Comments are closed.