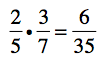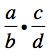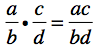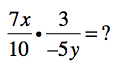Properties that are damaged by fire, water, storms, smoke, or mold require the services of a professional. This is a job for Nate Dawson, Restoration Hero and President of Sterling Restoration. Read on to see how he uses math to restore damaged properties back to mint condition.
Can you explain what you do for a living?
Sterling Restoration specializes in emergency repair to real property whether damaged by fire, water, storm, smoke or mold. Sterling Restoration is trusted for high quality and comprehensive cleanup, mitigation, and restoration services for both residential and commercial projects. We are a locally owned company based in Springfield, Ohio serving the Miami Valley and Central Ohio areas. We take pride in knowing that our team of professionals and extensive network of resources have the expertise to return any property to its pre-loss condition as quickly as possible.
When do you use basic math in your job?
Basic math is used in all aspects of our business including our accounting, estimating and production departments. Our accounting department uses it to calculate payroll, receivables, and payables. Our estimators use math more than anyone in our business. During the estimating process for reconstruction, we use square footage formulas (L x W) for calculating materials used, for example: subfloor framing, roof framing , insulation, drywall, painting, etc.. We use square yard formulas (L x W/9) for calculating vinyl floors and carpet. Basic algebra formulas are used for calculating rafter lengths based on the rise and run of roof slopes.
One of our most interesting uses of basic math, and one I will focus on going forward is with water mitigation (returning a structure to dry standard). Basically, drying a wet building! Once we determine the affected area we then use a cubic footage formula (L x W x H) along with the extent of saturation to know how much dehumidification is needed. Dehumidifiers are rated based upon how many pints of water they are capable of removing from the air within a specific amount of time (AHAM Rating). Therefore, depending on the type of dehumidification used and it’s rating, we are able to determine the number of dehumidifiers we need to dry a structure within the standards of our industry (S-500 ANSI approved standard). We also use the atmospheric readings to determine whether we are creating the desired conditions required to remove water from affected materials and to determine the effectiveness of our equipment. To do this we use the temperature and relative humidity to determine specific humidity (the weight of moisture p/lbs of air) and dew point (the temperature at which water vapor will begin to condense). The formula we use to determine the number of dehumidifiers needed is as follows:
Step 1 – Determine Cubic feet (CF).
Step 2 – CF/Class Factor(a low grain refrigerant dehu has a class factor of 40 in a class two loss) = # of AHAM pints needed.
Step 3 – AHAM points needed/Dehumidifier rating = number of dehumidifiers needed.
I know! It’s starting to sound a little complicated but it is all basic math.
Do you use any technology (like calculators or computers) to help with this math? Why or why not?
Absolutely! Even though we are in the building trade we are not in the dark ages. We use the most advanced estimating system designed specifically for the insurance restoration (property repair) business. After in-putting the dimensions into a sketch type format, this system automatically calculates all the square footages, cubic footages, and linear footages. The next step is to add a specific line item. For example, when you add drywall to your estimate it uses a current square foot price to calculate how much to charge for hanging, taping and finishing the drywall in your project. It will also calculate how many sheets of drywall, how many fasteners are needed , how much drywall tape, and how much joint compound is needed. Finally, it will calculate the material sales tax and any state sales tax on the service.
How do you think math helps you do your job better?
I do not feel it’s a matter of doing my job better. I simply could not perform my job without math! As I stated earlier, we use math in every aspect of our business. I do not feel there are too many moments throughout the day that I am not using some form of math.
What kind of math did you take in high school?
During my high school years I completed algebra and some trigonometry. If I remember correctly, that was all that was offered (yes, I graduated high school 32 years ago). Once leaving high school I furthered my math education in mechanical engineering. In my opinion, the levels of math being taught in high school today are far superior to what was then taught.
Did you like it/feel like you were good at it?
I feel like there are individuals that have an aptitude for math and those who do not. Math will obviously come easy for those who have this aptitude. I would also say that if you are good at something, the chances of enjoying it are far greater than if you are not good. Having said that, I do not believe I had this aptitude. Therefore, I had to work a little harder than others, and, at best, I was average at math. Guess where I’m going with this…no I did not like it.
Did you have to learn new skills in order to do the math you use in your job? Or was it something that you could pick up using the skills you learned in school?
I had to learn how to use the math skills I had already acquired to accomplish the task at hand. For example, if you have the lengths of two sides and the angle of a triangle, you can calculate the length of the third side. It is crazy how much I use this algebraic formula; however, it took some time and experience to learn how many applications this formula has. Having said that, ninety percent of my daily tasks require math learned in high school.
Are you interested in learning more about restoration? Let me know and I will pass your information along to Nate.