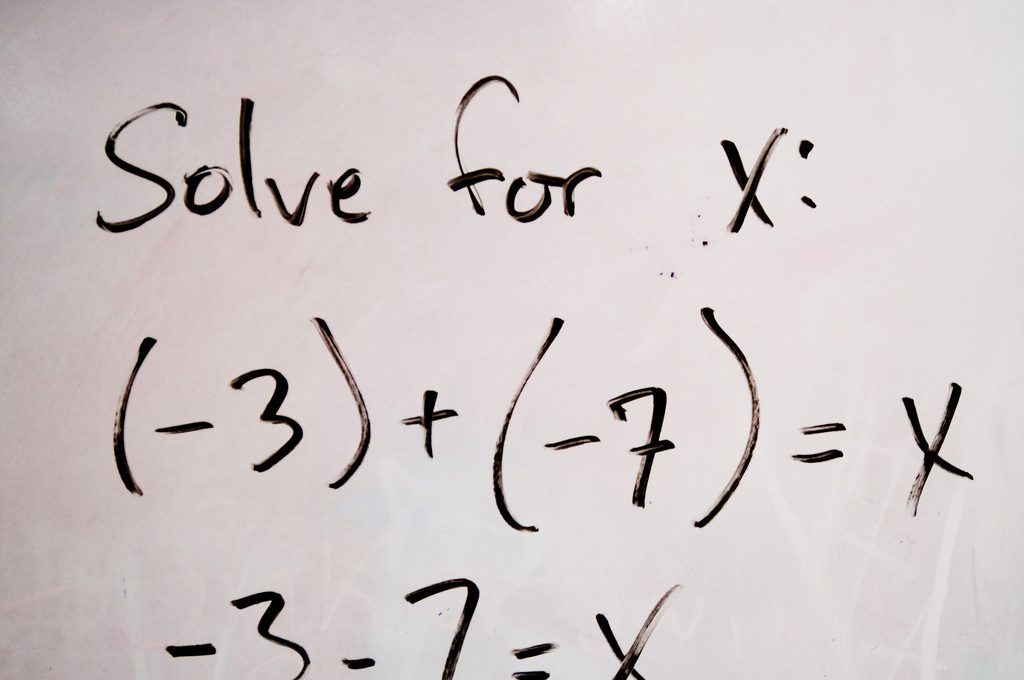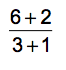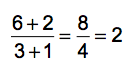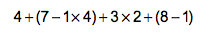teaching math Archives | Math for Grownups

In Math Education

The Problems with PEMDAS (and a solution)

If you’re on Facebook, you’ve probably seen one of a variety of graphics like the one above.

The idea is to solve the problem and then post your answer. From what I’ve observed, about half of the respondents get the answer correct, while the other half comes to the wrong answer. The root of this problem? The order of operations.

Unlike reading English, arithmetic is not performed from left to right. There is a particular order in which the addition, subtraction, multiplication, and division (not to mention parentheses and exponents) must be done. And for most of us old-timers, that order is represented by the acronym PEMDAS (or its variations).

P – parentheses
E – exponents
M – multiplication
D – division
A – addition
S – subtraction

I learned the mnemonic “Please Excuse My Dear Aunt Sally” to help me remember the order of operations.

The idea is simple: to solve an arithmetic problem (or simplify an algebraic expression), you address any operations inside parentheses (or brackets) first. Then exponents, then multiplication and/or division and finally addition and/or subtraction.

But there really are a lot of problems with this process. First off, because multiplication and division are inverses (they undo one another), it’s perfectly legal to divide before you multiply. The same thing goes for addition and subtraction. That means that PEMDAS, PEDMSA, and PEMDSA are also acceptable acronyms. (Not so black and white anymore, eh?)

Second, there are times when parentheses are implied. Take a look:

If you’re taking PEMDAS literally, you might be tempted to divide 6 by 3 and then 2 by 1 before adding.

Problem is, there are parentheses implied, simply because the problem includes the addition in the numerator (top) and denominator (bottom) of the fraction. The correct way to solve this problem is this:

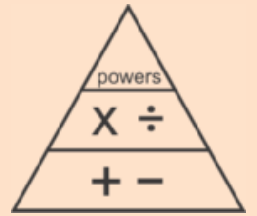
So in the end, PEMDAS may cause more confusion. Of course, as long-time Math for Grownups readers should know, there is more than one way to skin a math problem. Okay, okay. That doesn’t mean there is more than one order of operations. BUT really smart math educators have come up with a new way of teaching the order of operations. It’s called the Boss Triangle or the hierarchy-of-operations triangle. (Boss triangle is so much more catchy!)

The idea is simple: exponents (powers) are the boss of multiplication, division, addition, and subtraction. Multiplication and division are the bosses of addition and subtraction. The boss always goes first. But since multiplication and division are grouped (as are addition and subtraction), those operations have equal power. So either of the pair can go first.

So what about parentheses (or brackets)? Take a close look at what is represented in the triangle. If you noticed that it’s only operations, give yourself a gold star. Parentheses are not operations, but they are containers for operations. Take a look at the following:

Do you really have to do what’s in the parentheses first? Or will you get the same answer if you find 3 x 2 first? The parentheses aren’t really about the order. They’re about grouping. You don’t want to find 4 + 3, in this case, because 4 is part of the grouping (7 – 1 x 4). (Don’t believe me? Try doing the operations in this problem in a different order. Because of where the parentheses are placed, you’re bound to get the correct answer more than once.)

And there you have it — the Boss Triangle and a new way to think of the order of operations. There are many different reasons this new process may be easier for some children. Here are just a few:

1. Visually inclined students have a tool that suits their learning style.

2. Students begin to associate what I call the “couple operations” and what real math teachers call “inverse operations”: multiplication and division and addition and subtraction. This helps considerably when students begin adding and subtracting integers (positive and negative numbers) later on.

3. Pointing out that couple operations (x and ÷, + and -) have equal power allows students much more flexibility in computing complex calculations and simplifying algebraic expressions.

Even better, knowing about the Boss Triangle can help parents better understand their own child’s math assignments — especially if they’re not depending on PEMDAS.

So what do you think? Does the Boss Triangle make sense to you? Or do you prefer PEMDAS? What to learn to solve these and other problems, buy the book that will help grown-ups like you with these and other math problems here.

In Math Anxiety

X to the Power of Huh? Or, How Math Anxiety Almost Ruined My Life

I’m betting that many of you dear readers will identify with today’s guest post from Lisa Tabachnick Hotta. Math anxiety may still dog some of us, but it doesn’t have to ruin our lives. Read my guest post on her blog here.

“Miss Tabachnick,” exclaimed my grade 8 math teacher. “Please come up to the board and demonstrate how you obtained the answer to that equation; I’m sure the entire class will benefit from your explanation.”

Sweat trickled its way from my brow to my toes. Show the class? Now? At the chalk board? Somehow I must’ve squeaked out the answer because I did graduate – from grade 8, then from high school and ultimately obtained two university degrees. (My majors, of course, had absolutely nothing to do with math!)

Anxiety in all its sweaty glory – shaky hands, racing pulse, nausea – is pretty much the story of my life when it comes to math. Of course I’m rarely at a chalk (or smart) board deciphering mathematical problems these days as a writer, community volunteer and parent. But, you will often find me deep in “grownup” math conundrums. Here are but a few examples:

Recently I was out for dinner with the girls and we were splitting the check. “Anne, you’re the accountant, you can figure out what we all owe,” I half-joked to one member of our group. She wasn’t amused. (Maybe it’s like the doctor who’s always getting asked for health tips at parties?) Her reluctance to assist me meant having to figure out not only what my drink, dinner and dessert cost but also my portion of the tax and tip – not at all easy for someone who’s math challenged!
My son who is (miraculously) gifted in math, asked me fairly simple questions in the car as a kind of numbers game: What’s 2 + 2, What’s 4 + 4, What’s 8 + 8, What’s 16 + 16, etc. Now, the first few questions? No problemo. But, as the numbers and queries got larger, I had to think harder to come up with the answers and, yes, that in turn increased my anxiety level.
Just today my kids and I were at a medical appointment. The administrator explained that receiving a response from the government to our query could take up to 30 weeks. I laughed along with the other adults who joked about government inefficiencies but, somewhere in my mind, I was still trying to figure out how many months equalled 30 weeks.

All joking aside, being mathematically challenged has caused me enormous stress. From hiring tutors throughout middle and high school, to being told (by that same grade 8 math teacher) that I’d never amount to anything because my math skills were so poor, to ensuring that I am charging clients appropriate rates on invoices – I’ll be forever haunted by issues around math.

So, how do I cope as a math-phobic adult? Luckily, I’ve learned to lean on my strengths – writing, communications and art. I also lean on calculators! Have you heard the expression, “fake it ‘til you make it”? I’ve also employed that strategy more than once. And, I’ve found that humor works well – I’ll just admit outright that math isn’t my forte and, while I’d be happy to volunteer as project manager or group leader, appointing me treasurer really isn’t the best idea.

Lisa Tabachnick Hotta is a professional writer, editor, social media expert and researcher who lives just north of Toronto, Ontario. Lisa specializes on topics related to health, mental health, family, the arts and society. Check out her blog: KidsAndMentalHealth.com.

What are your childhood memories of math anxiety? How does math anxiety influence your life now? How have you learned to get around it?

In Math at Work Monday

Math at Work Monday: Tiffany the 6th grade teacher

I know what you’re thinking. “It’s so obvious how a 6th grade teacher would use math! She’s teaching fractions and division and percents!”

There’s always a lot more to teaching than the rest of us may think. And that’s why I asked Tiffany Choice to answer today’s Math at Work Monday questions. Ms. Choice was my daughter’s 4th grade teacher, and she’s the best elementary math teacher I’ve ever met. She truly made the math fun, and she really got into her lessons. I know this for sure, because I had the pleasure of subbing for Ms. Choice while she was on maternity leave. Let me tell you, those kids loved her — and so do I!

Last year, Ms. Choice moved to Fairfax County, Virginia. She’s getting ready to start teaching 6th grade there. In honor of what was supposed to be our first day of school — until Hurricane Irene changed our plans! — here’s how she uses math in her classroom.

Can you explain what you do for a living? I teach state-mandated curriculum to students. My job also includes communicating to parents progress and/or concerns, appropriately assessing my students, and analyzing data to drive my instruction and lessons.

When do you use basic math in your job? I use math all the time — mostly basic addition, subtraction, multiplication and division. When I plan lessons, I need to appropriately plan for activities that will last a certain length of time. Then, when I am teaching the lessons, I am watching the clock and using timers to keep my lessons moving or calculating elapsed time.

I also use math to grade assignments and calculate grades. I break a student’s grade into 4 categories; participation, homework, classwork, test/projects. Each category has a different weight. Participation and homework are each 10 percent, while classwork and test/projects are each 40 percent. Then for each grading period, I average grades and take the appropriate percentage to get the overall grade.

I also use math to analyze data and drive my instruction. After quarter assessments or chapter tests are given, I look for trends. Which questions did the majority of students get incorrect? If I notice out of 60 students only 30% of them got a certain question correct this says to me that most of them (42 to be exact) got the question wrong. I need to figure out why and go back.

I will also use math to group my students for games and activities. When I originally plan for them I always assume all students will be present. However, with absences and such I have to use last-minute division to regroup them. I move desks around into different groups periodically during the year, and that requires division as well.[pullquote]It’s completely normal to feel anxious or nervous about math. But a great teacher at any level (primary to college) will help you “get it.” Just don’t give up.[/pullquote]

When I plan for field trips, I have to calculate the total cost for each student depending on the fees involved. Then, I have to count large amounts money that has been collected to account for the correct amounts.

Do you use any technology (like calculators or computers) to help with this math? At my first teaching job, I had a computer program that calculated grades for me, but when I left and went to a new district I didn’t have that software, so I did grades all by hand using a calculator.

How do you think math helps you do your job better? The whole point of my job is to get students to learn and become great thinkers. I wouldn’t be able to find or focus on areas of weakness if I wasn’t able to properly analyze data and comprehend what it really means to me.

What kind of math did you take in high school? Did you like it or feel like you were good at it? I only took algebra and geometry in high school. I was terrible at math in high school and didn’t enjoy it or “get it” until college. I started in a community college and I had to take two developmental math classes before I could take what was required. It was during those developmental courses I finally “got it” and began to actually enjoy it. Everything finally made sense.

It’s completely normal to feel anxious or nervous about math. But a great teacher at any level (primary to college) will help you “get it.” Just don’t give up.

Did you have to learn new skills in order to do this math? The math I use to do my job is math that is taught up to the middle school level. I didn’t have to learn anything special.

Thanks so much, Ms. Choice! (I don’t think I can ever call her Tiffany!) If you have questions for Ms. Choice, just ask them in the comments section. She has agreed to come back to Math for Grownups to talk a bit about how parents can work with their kids’ math teachers, so stay tuned for more advice from her.

In Math for Parents

Film Friday: When will I ever use this stuff?

It’s the perennial question from students of all ages: “When will I use this stuff?” So when tutor, Ryan faced this query (probably for the upteenth time), he took to the streets to find the answer. What he found is in the video below:

And of course I have some thoughts — for teachers and students.

It is absolutely true that series (that’s what the funny looking E — an uppercase sigma — means in this problem) are not the stuff of ordinary folks in non-science fields. But they’re not as difficult as they seem. It’s the notation that’s confusing.

Skip this part, if you don’t really want to do any algebra today.

A series is just the sum of a sequence (or list) of numbers. That’s it. Nothing more, nothing less. So when you have

sum{n=1}{7}{3n-1}

you’re simply saying, “Find the sum of the first 7 values of 3n-1, where the first value of n is 1.” In other words: 2 + 5 + 8 + 11 + 14 + 17 + 20 = 77.

Now back to my opinions.

Okay, so I don’t need to know what a series is in order to visit the grocery store or get a good deal on a car or even figure out how much I earned this year over last year. But here’s what I wish some of those folks who were interviewed for this video had been able to say:

“That funny-looking E is a Greek letter, right?”

“Doesn’t this have to do with adding things together?”

“Hey, I dated a girl from {Sigma}{Sigma}{Sigma} once!”

And second, this tutor did pick a humdinger of a problem to focus on. Series (and their brothers, sequences) are not the main focus of any mathematics course. But honestly, they wouldn’t be taught if they weren’t useful somewhere. And boy-howdy are they useful!

So, here are a few ways that real people do use series in their real jobs (courtesy of Algebra Lab and Montana State University:

1. Architecture: “An auditorium has 20 seats on the first row, 24 seats on the second row, 28 seats on the third row, and so on and has 30 rows of seats. How many seats are in the theatre?”

2. Business: “A company is offering a job with a salary of $30,000 for the first year and a 5% raise each year after that. If that 5% raise continues every year, find the amount of money you would earn in a 40-year career.”

3. Investment Analysis: “A person invests $800 at the beginning of each year in a superannuation fund. Compound interest is paid at 10% per annum on the investment. The first $800 was invested at the beginning of 1988 and the last is to be invested at the beginning 2017. Calculate the total amount at the beginning of 2018.”

4. Physics: “The nucleii of a radioactive isotope decay randomly. What is the total number of nucleii after a given period of time?”

And this brings me to some additional news of the week. Sol Garfunkel (Consortium for Mathematics and Its Applications) and David Mumford (emeritus professor of mathematics at Brown) made a bit of a splash on Wednesday, with an editorial in the New York Times: How to Fix Our Math Education.

Their proposal is that we teach tons of math that applies to everyday life — and focus on those applications. (Yay!) And we ditch “highly conceptual” math for folks who won’t need it for their jobs. (Boo!)

Hopefully, you’ve already identified the problem: How do we know if a kid won’t decide to go into physics or engineering or high school math education? Hell, how do we even attempt to lure them into these fields, if they don’t see the math at all? (And by the way, physics, engineering and applied mathematics were recently identified as the top-paying degrees in the U.S.)

Look, I empathize with the student who isn’t interested in what any of the Greek letters mean in math class. And I think it’s true that most folks won’t use these skills at all after high school. (It is worth mentioning that everyone depends on series in their daily lives–they just don’t see the math.) But my response to the kid who asks, “What’s this good for?” is to tell him where it can be applied.

And if he says he won’t be going into any of those fields, I would say, “Suck it up, cupcake, because you’re too darned young to know for sure.”

Please share your thoughts in the comments section. Do you agree that these concepts should be taught in high school, even though most kids won’t use them in their everyday lives? How do you think we should encourage more students to go into science, technology, engineering and math (STEM) fields?

In Math Anxiety

Get the Anxiety Out of Math

“Math is fun power” Photo courtesy of dtweney.

Things that make many kids anxious: a new school, big dogs, the deep end of the swimming pool, bees, strangers, nightmares, math.

Did you notice something there? For many children, math and bees are equally frightening or at least nerve-wracking.

Not all kids have math anxiety, but it’s not uncommon for elementary, middle or high school students to express nervousness about learning math or taking math tests. At the same time, these students may also feel less confident in their math skills or even say that they hate math.

Want to know how to eleviate math anxiety–for your kids and yourself? Check out my guest post at Imp3rfect Mom. You could win a free copy of Math for Grownups!Would you like me to guest post at your blog? Or do you know of a blog that I would fit right in with? I’ve got lots of ideas to share with anyone who will listen! And I promise I’m a good guest. I wipe out the sink after I brush my teeth and don’t mind if the cat sleeps on my pillow. Get the details here.

In Math for Parents

Math Secret #2: You Were Born This Way (take 2)

All summer long, we’ve seen some pretty amazing research on math ability and education. We’ve been told that understanding geometric concepts may be innate and that elementary-aged students with a good sense of numeracy do better in math by the 5th grade. And yesterday news of another study hit the internet.

According to the headlines, we were born either good or bad at math. At least that’s how this study is being interpreted by bloggers and news outlets. Except that’s not necessarily what the study concludes.

This makes me mad. Really mad. I have not read the full study, but nothing in the abstract–or even the stories and blog posts about this study–suggests that people are born with or without math ability. Instead, it seems that the cheeky headlines were just too good to pass up.

Here’s what the study author, post-doctoral student Melissa Libertus, does say:

The relationship between ‘number sense’ and math ability is important and intriguing because we believe that ‘number sense’ is universal, whereas math ability has been thought to be highly dependent on culture and language and takes many years to learn… Many questions remain and there is much we still have to learn about this.

And here’s the nitty gritty on the study itself. A group of 200 children, with an average age of 4 years old, was given a number sense test. (You can take the exact same test here). These children were then asked to perform a variety of age-appropriate math tasks, including counting, reading numbers and computations. The results make a lot of sense: children who performed well on the number sense test did better on the math tests.[pullquote]No one says that we’re born good or bad at reading. We’re all expected to learn to read–and read well. So why do we say that about math?[/pullquote]

But the results seem to be misrepresented by media and others. These kids were selected precisely because they haven’t had any formal math education. They’re preschoolers. So, according to many news reports, kids are either born with number sense or get it from formal education.

Rubbish.

If you had a child in the last 10 or 15 years–or know someone who has–you are probably familiar with the big, big push for early literacy. Parents are encouraged to read to their kids, even when they’re babies, which research has shown helps the children develop age-appropriate literacy skills. In fact, kids who have had access to pre-reading experiences as infants, toddlers and preschoolers do much better with reading in elementary school. (This is one of the tenets of Head Start programs around the country.)

No one says that we’re born good or bad at reading. We’re all expected to learn to read–and read well. So why do we say that about math?

Just like the researcher, I think this study raises more questions. And here’s the really big one: What can parents do to boost their kids’ numeracy before formal education begins? (I actually wrote about this earlier this week.)

I still maintain that we are born with an innate understanding of math–just like we’re born knowing something about language. But without stimulating this understanding, kids can fall behind their peers or at least not reach their full potential. We read to little children so that they can learn to read on their own. And we should be doing something similar with kids so that they can do math.

A friend and fellow math blogger, Bon Crowder has launched an amazing program she’s calling Count 10, Read 10. It’s a simple idea: Parents should spend 10 minutes each day reading to their young kids and 10 minutes doing some sort of math with them. But nobody is saying flash cards, worksheets or chalkboards are necessary. The trick is to sneak the math into everyday activities, which can be as simple as counting the steps your new walker takes.

So here’s what I think happened with the news reports of this study: reporters, editors and bloggers simply tapped into their own misconceptions about math–and even their own math anxiety–and distorted the message. For many people, it’s a “fact” that some people are just naturally bad at math. I hope you’ll help me challenge that notion.

Meanwhile, be careful what you read.

P.S. A great math educator, David Wees has also chimed in on this topic, and shares–more eloquently–some of the same concerns I have. Read it!

So what do you think? Are people born good or bad at math? Can parents help develop numeracy in their children? How? Share your ideas in the comments section.

In Math for Parents

When It Comes to Math, Parents Should Chill

What’s the one thing most parents have in common? We push our kids. “Eat your veggies.” “Do your homework.” “Unload the dishwasher.” And even though it sounds like nagging, these lessons are the ones that help our kids grow into successful adults.

But when it comes to math, are you doing all that you can to ensure that your child or teen will be successful? Do you even know what those things are? The best advice may actually be surprising.

Turns out, there are a few very simple steps you can take that will make a huge difference in how your child performs in mathematics and perceives his or her math skills.

Are you worried about your child’s math skills? Relax and read the rest of my guest post at Flynn Media.

By the way, would you like me to guest post at your blog? Or do you know of a blog that I would fit right in with? I’ve got lots of ideas to share with anyone who will listen! And I promise I’m a good guest. I wipe out the sink after I brush my teeth and don’t mind if the cat sleeps on my pillow. Get the details here.

In Math Education

Is Math a Foreign Language?

When I was in college, majoring in math education, I learned that math is the language of science. In fact, we called it the Queen of the Sciences. (You’d better believe that gave me a sense of superiority over the chemistry and physics majors!) And yeah, I think that the math I was doing then–calculus, differential equations, statistics and even abstract algebra–is mostly useful for describing some kind of science. [pullquote]We too often think of mathematics as rules rather than as questions. This is like thinking of stories as grammar. — Rick Ackerly[/pullquote]

In some ways, everyday math is also the language of science. Home cooks use ratios to ensure that their roux thickens a gumbo just right. With proportions, gardeners can fertilize their vegetable beds without burning the leaves from their pepper plants. And a cyclist might employ a bit of math to find her rate or the distance she’s biked.

But I think too often we adults get caught up in the nitty gritty of basic math and lose the big picture. This is when many of us start to worry about doing things exactly right–and when math feels more like a foreign language, rather than a useful tool.

Earlier this week, I read a blog post from Rick Ackerly, who writes The Genius in Children, a blog about the “delights, mysteries and challenges of educating our children.” In Why Mathematics is a Foreign Language in America and What to Do about It, he writes:

Why do Americans do so badly in mathematics? Because mathematics is a foreign language in America. The vast majority of children grow up in a number-poor environment. We’ve forgotten that the language of mathematics is founded in curiosity. We too often think of mathematics as rules rather than as questions. This is like thinking of stories as grammar. Being curious together can be a really special part of the relationship in families.

And I couldn’t agree more. For all of you parents and teachers out there: how many questions do your kids ask in one day? 10? 20? 100? 1,000? As Ackerly points out, especially younger children are insatiably curious. They want to know why the sky is blue and what makes our feet stink and how come that ladybug is on top of the other ladybug.

These Stevendotted ladybugs are not wrestling. Photo credit: Andr Karwath

A full 90% of the time, we can’t answer their questions. Or maybe we just don’t want to yet. (“That ladybug is giving the other one a ride.”) With Google‘s help, we can find lots of answers. But how often are we asked a math-related question–by a kid or a grownup–and freeze?

For whatever reason, many people are afraid to be curious about math. Or they’ve had that curiosity beaten out of them. I think that’s because don’t want to be wrong. As fellow writer, Jennifer Lawler said to me the other day:

It’s funny because when I make a mistake in writing—a typo, etc.—I let myself off the hook (“Happens to everyone! Next time I’ll remember to pay more attention.”) But if I misadd a row of numbers I’m all “OMG, I’m such an idiot, and everyone knows I’m such an idiot, I can’t believe they gave me a college degree, and why do I even try without my calculator?”

The same goes for answering our kids’–or our own–calls of curiosity.

So what if we decided not to shut down those questions? What if it was okay to make some mistakes? What if we told our kids or ourselves, “I don’t know–let’s find out!” This could be a really scary prospect for some of us, but I invite you to try.

What’s keeping you from being curious about everyday math? What do you you think you can do to change that? Or do you think it doesn’t matter one way or the other? Share your ideas in in a comment.

In Math Education

Mixing in Math: Teacher Cooks Up Lesson in the Kitchen

So this apparently is big news in Myrtle Beach. A middle school math teacher actually took her kids out of the classroom to teach them math. In the school cafeteria, the students converted decimals to percents and found surface area and volume — as they were cooking up some healthy eats.

Ya’ll, seriously. This is what how we use math as grownups.

(Okay, so the surface area and volume is a bit of a stretch.)

If you think doing math is about chalkboards and protractors, you’re flat out wrong. (Besides schools use dry erase boards these days.)

Math is about getting your hands dirty, sketching a picture on a scrap piece of paper, doing some quick calculations on the iPhone. Most of all, math is about solving real problems — not those silly things that have something to do with trains in Omaha — and coming to these solutions in creative and sensible ways. (There. I said it: creative and sensible.)

Look, I like what this teacher is doing. And so do her students:

“You learn it better because you enjoy doing it,” said Maya Bougebrayel, who made a vegetable chicken stir fry with teammates Allison Klein and Carlisa Singleton. The girls, all 13, agreed that the project put a creative spin on learning and made it easier for those who are visual learners.

But if it wasn’t such a novel idea, wouldn’t grownups be better at math? Feel free to chime in in the comments section.