If you’re on Facebook, you’ve probably seen one of a variety of graphics like the one above.
The idea is to solve the problem and then post your answer. From what I’ve observed, about half of the respondents get the answer correct, while the other half comes to the wrong answer. The root of this problem? The order of operations.
Unlike reading English, arithmetic is not performed from left to right. There is a particular order in which the addition, subtraction, multiplication, and division (not to mention parentheses and exponents) must be done. And for most of us old-timers, that order is represented by the acronym PEMDAS (or its variations).
P – parentheses
E – exponents
M – multiplication
D – division
A – addition
S – subtraction
I learned the mnemonic “Please Excuse My Dear Aunt Sally” to help me remember the order of operations.
The idea is simple: to solve an arithmetic problem (or simplify an algebraic expression), you address any operations inside parentheses (or brackets) first. Then exponents, then multiplication and/or division and finally addition and/or subtraction.
But there really are a lot of problems with this process. First off, because multiplication and division are inverses (they undo one another), it’s perfectly legal to divide before you multiply. The same thing goes for addition and subtraction. That means that PEMDAS, PEDMSA, and PEMDSA are also acceptable acronyms. (Not so black and white anymore, eh?)
Second, there are times when parentheses are implied. Take a look:
If you’re taking PEMDAS literally, you might be tempted to divide 6 by 3 and then 2 by 1 before adding.
Problem is, there are parentheses implied, simply because the problem includes the addition in the numerator (top) and denominator (bottom) of the fraction. The correct way to solve this problem is this:
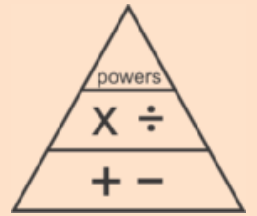
So in the end, PEMDAS may cause more confusion. Of course, as long-time Math for Grownups readers should know, there is more than one way to skin a math problem. Okay, okay. That doesn’t mean there is more than one order of operations. BUT really smart math educators have come up with a new way of teaching the order of operations. It’s called the Boss Triangle or the hierarchy-of-operations triangle. (Boss triangle is so much more catchy!)
The idea is simple: exponents (powers) are the boss of multiplication, division, addition, and subtraction. Multiplication and division are the bosses of addition and subtraction. The boss always goes first. But since multiplication and division are grouped (as are addition and subtraction), those operations have equal power. So either of the pair can go first.
So what about parentheses (or brackets)? Take a close look at what is represented in the triangle. If you noticed that it’s only operations, give yourself a gold star. Parentheses are not operations, but they are containers for operations. Take a look at the following:
Do you really have to do what’s in the parentheses first? Or will you get the same answer if you find 3 x 2 first? The parentheses aren’t really about the order. They’re about grouping. You don’t want to find 4 + 3, in this case, because 4 is part of the grouping (7 – 1 x 4). (Don’t believe me? Try doing the operations in this problem in a different order. Because of where the parentheses are placed, you’re bound to get the correct answer more than once.)
And there you have it — the Boss Triangle and a new way to think of the order of operations. There are many different reasons this new process may be easier for some children. Here are just a few:
1. Visually inclined students have a tool that suits their learning style.
2. Students begin to associate what I call the “couple operations” and what real math teachers call “inverse operations”: multiplication and division and addition and subtraction. This helps considerably when students begin adding and subtracting integers (positive and negative numbers) later on.
3. Pointing out that couple operations (x and ÷, + and -) have equal power allows students much more flexibility in computing complex calculations and simplifying algebraic expressions.
Even better, knowing about the Boss Triangle can help parents better understand their own child’s math assignments — especially if they’re not depending on PEMDAS.
So what do you think? Does the Boss Triangle make sense to you? Or do you prefer PEMDAS? What to learn to solve these and other problems, buy the book that will help grown-ups like you with these and other math problems here.

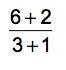
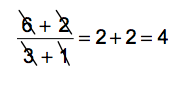
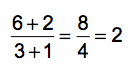
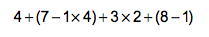





Comments are closed.