Math is black-and-white, with right-or-wrong answers. It’s hard to color outside the lines in math.
While I often argue with this point, there is some truth to it. Just like grammar, chemistry and baking, math is a pretty precise subject matter. Sure, there are many different ways to add 24 and 37 in your head, but fact is, you can’t just decided that the answer is –19, right?
Rules make math work. And algebra helps us write down these rules. Now, we don’t necessarily need to think of math rules in this way, but believe me, when teaching and writing about math, it sure does help. And there are some real-world situations when an equation can really help make math easier.
Let’s consider the process for multiplying fractions. Do you remember what it is? Take a look at this problem, and see if you can figure it out:
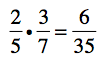
Of course there are several ways to describe what is happening above, right? You can do it in plain English:
To multiply two fractions, multiply the numerators and multiply the denominators.
Or, you can write this using algebra. This is not as hard as you might think! First, assign a variable to each of the unique numbers on the left side of the equation:
a = first numerator
b = first denominator
c = second numerator
d = second denominator
Then substitute those variables for the numbers themselves:
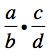
Now, perform the rule that was described in plain English above: multiply the numerators and multiply the denominators.
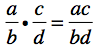
How about that! Lickity split, we made like mathematicians and created a rule described algebraically. How hard was that really?
Now you can use this rule to multiply any fractions of any kind. I don’t care if they’re elementary fractions made up of just numbers or if they’re fancy-schmancy algebraic functions that have — gasp! — variables in them. You don’t even have to think of the a, b, c or d. Instead, think of those variables as place holders. (Hint: this is where your mind can be really flexible, even though the rule is not.)
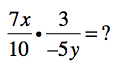
Because you know this rule, you can solve this problem (even with the x and the y). Just multiply the numerators and then multiply the denominators.
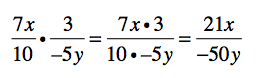
Because of the rule for multiplying fractions — which includes the variables a, b, c and d — you can see how to multiply any fractions. That’s where the algebra comes in handy.
Now, I know exactly what you’re thinking. When will I ever need to solve a problem like the one above. And here’s my honest answer: for most of you, never. Really and truly. I won’t lie.
However, there are times when creating a rule for a specific real-word problem is very useful. That’s when we might create an equation. Stay tuned, when we’ll talk wedding receptions, guest lists, the price per person and rental fees.
So what do you think of algebra and math rules? Did this example help you understand how algebra is important in developing and stating these rules? Do you disagree with me about why this is important? I can take it — so please do share your thoughts in the comments section.
