Categories
Ask a Math Teacher

What Does “Hundreds” Mean?

Welcome to the first edition of Ask a Math Teacher, which will feature real, live math questions from real, live people. How often will I do this? As often as I can. What kinds of questions can you expect? Whatever people ask. If you have a question, please post it to the Math for Grownups Facebookpage (after clicking “like” of course!) or email me at lelaing-at-gmail-com.

Today’s question comes from my friend and cookbook author, Debbie Koenig. You really should check out her blog and book, Parents Need to Eat Too. Debbie posted this question on Facebook, which led to a two-day long post-a-thon. We finally got to the root of the question — and answer — and I thought you would like to hear about it.

My son’s math homework has me scratching my head–he’s supposed to “Draw a picture of 600 hundreds” in a space that’s maybe an inch and a half high. How does one draw 600 of anything in that small a space? And why is he drawing 600 of something? I have no idea how to help him. 

One thing that isn’t clear in this question is that her son is in second grade. This is a really important piece of information, because the answer is going to seem completely counter-intuitive to us grownups.

Some background: When children learn their numbers and then learn to count and then learn to write 3s, 7s and 4s (sometimes backwards), they are picking up teeny-tiny bits of number sense. When all of this information is put together, we call that numeracy. You can think of numeracy like literacy. It’s not just being able to count or add; it’s being able to understand how numbers work together in a much larger sense. As you can imagine, this is a big, hairy deal. It takes years and years to get to where we adults are. And most of us grownups take for granted the numeracy that we do have.

I say this because what this “hundreds” thing is getting at is place value, or the position of a digit in a number. Teachers can just tell students that the 4 in 9433 is in the tens place, or — and this is a muchbetter idea — students can learn a great deal more about numbers by really exploring this concept.

You see, place value is not some random construct. There are reasons that the first place to the right of a decimal is the ones place and the fourth place to the right of the decimal is the thousands place. Exploring this can help kids get better at multiplying or dividing and lay the foundation for decimals and even percentages.

So with that said, the first thing to do is ignore what you think hundreds means. Unless you’ve had some experience in math education, you’re probably not going to take the right guess. In second-grade math class, hundreds does not mean one hundred. It means the hundreds place.

The easiest way to get into this is by looking at a hundreds chart.

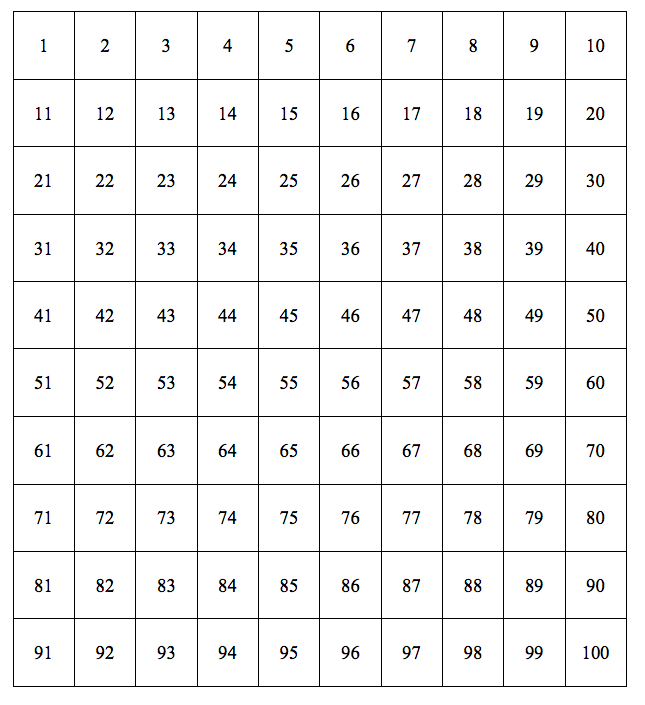
If you have one of these hundred charts, you have 100, right? How can you represent 600 then? I’ll give you a second to think about it…

Yep, with six of these buggers! Here’s a visual representation without the numbers:

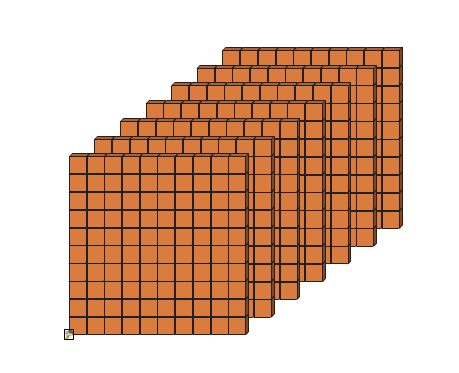
So what Debbie’s son was being asked to do was draw something like the above. It’s important because it has to do with place value. Only most second graders don’t have a clue about that stuff yet. And what they have learned so far sounds like a big mistake to the rest of us — because the language being used is not what we expect. He’ll learn the word “place value” in due time and forget about these hundreds tiles and charts and suchlike.

Asking students to draw “600 hundreds” is helping students visualize place value and other important concepts. Teachers call these manipulatives, especially because they’re often real objects that students can pick up and move around. But on a homework worksheet, they’re a little harder to translate, especially for a parent who went to elementary school more than a few years ago.

So that’s the story of “hundreds,” at least as far as a second grader is concerned. I’d love to hear your thoughts! Do you know of other ways to get to the basics of place value? Do you, personally, think of place value differently? Share in the comments section.

P.S. I’m going to be speaking to parents of elementary-aged kids at my daughter’s school later this month. If you have questions that you think I should address, feel free to shoot me a quick note or post on the Math For Grownups Facebook Page. And if your school — in the D.C.-Baltimore area — would like to have me come down for a Math Chat, let me know. I’d love to meet you!

Categories
Basic Math Review Math for Grownups Math for Parents Math for Teachers

Five Cool Math Tricks You Didn’t Know

When it comes to basic calculations, kids can benefit from knowing math facts cold. When the arithmetic is simple, we can focus on more complex concepts.

That’s one reason your children are encouraged to memorize their multiplication tables. But over the years, educators have discovered that straight memorization is not always the best. In fact, when kids spend a great deal of time really unpacking what these math concepts mean, they’re far more likely to expand their understanding of many other concepts.

So are math “tricks” a good thing or a bad thing?

“Kids should have a way of figuring out the math fact that uses reasoning,” says Dr. Felice Shore, assistant professor and co-assistant chairperson of Towson University’s math department in Maryland. As an expert in mathematics education, Shore knows that when children’s natural curiosity is stimulated, they can make important mathematical connections that will deepen their understanding.

“But once kids can reason their way to the answer and understand various ways to do so, these ‘tricks’ can help them get answers quickly,” she continues.

The key is to introduce these tricks at the right age.

“I don’t think the third or even fourth-graders should learn tricks,” Shore says. “The important mathematics at those grades is still about building an understanding of relationships between numbers—the very reasons behind math facts. Once you show them the trick, it’ll most likely just shut down their thinking.”

But math tricks can be useful. If your fifth grader is still struggling with her multiplication tables, these can be a godsend. Even better is when they reveal something about the math that makes them work.

If you’re going to show your child a quick way to multiply, make sure that you help her understand why the trick works. Here are five cool examples—and the math behind them.

[laurabooks]

Multiplying by 4

This trick is so simple and logical, that it could hardly be called a trick. But it could come in handy for your budding Sir Isaac Newton. To multiply any number by 4, simply multiply it by 2 and then double the answer.

35 x 4
35 x 2 = 70
70 x 2 = 140
35 x 4 = 140

Why does it work?

This trick is based on a very simple fact:

2 x 2 = 4

That means that:

35 x 4 = 35 x (2 x 2)

And

35 x 2 x 2
70 x 2
140

The underlying lesson of this “trick” is that you can solve a multiplication problem by multiplying by its factors.

Multiplying by 9

Hold up both hands, with your fingers spread. To multiply 4 x 9, bend your fourth finger from the left. Count the number of fingers to the left of your bent finger—you should get 3. Then count the number of fingers (and thumbs) to the right of your bent finger—you should get 6. The answer is 36. This works when multiplying any number 1-10 by 9.

Why does it work?

Simple algebra can show that what you’re doing with your fingers boils down to this: When you multiply by 9, you’re really multiplying by 10 and then subtracting that number. But you don’t need to do the algebra. Some kids figure out that reasoning without the mysterious finger trick.

You can help your child extend her understanding of the number 9 by pointing out an important piece of this trick: in the 9s multiplication tables, the digits add up to 9!

4 x 9 = 36   —>   3 + 6 = 9

9 x 9 = 81   —>  8 + 1 = 9

Then you can prompt your child to notice other patterns. For example, 4 -1 = 3 and 3 + 6 = 9 and 4 x 9 = 36. The patterns in the 9s multiplication tables are endless and can lead to many other discoveries about numbers.

Multiplying by 11

Sure, multiplying a one-digit number by 11 is a cinch.

4 x 11 = 44
7 x 11 = 77

But did you know there’s a trick to multiplying any number by 11?  Here’s how using an example: 52 x 11.

The first digit of the answer will be 5 and the last digit of the answer will be 2. To get the digit between, just add 5 and 2.

5 (5+2) 2
572

You may have noticed that when you add the two digits together, you get a one-digit number. If you get a two-digit number, things are a little trickier.

87 x 11
8 (8+7) 7
8 (15) 7
(8+1) 57
957

Why does it work?

If you think of doing long-hand multiplication by stacking the two numbers, you’ll see right away:

But the more precise reasoning has to do with place value. What you’re really doing is multiplying 87 by 1, then multiply 87 by 10, and finally adding the two products together:

87 x 1 = 87
87 x 10 = 870
870 + 87 = 957

The trick itself is just a shortcut to the answer.

Multiplying by 12

Just like the previous track, you can multiply any number by 12 very quickly and easily. Let’s try it with 7 x 12.

First multiply 7 by 10. Then multiply 7 by 2. Finally, add them together.

7 x 12
7 x 10 = 70
7 x 2 = 14
70 + 14 = 84

Easy peasy. When this gets really impressive is with larger numbers.

25 x 12
25 x 10 = 250
25 x 2 = 50
250 x 50 = 300

Why does it work?

This trick works for the same reason that the 11s trick works. But there’s another way to describe it. Think of 12 as the sum of 10 and 2.

25 x 12
25 x (10 + 2)
(25 x 10) + (25 x 2)
250 + 50
300

Is a number divisible by 3? (Or in math terms: Is a number a multiple of 3?)

When a number is evenly divisible by another number it is said to be a multiple of that number. In other words: since 27 is evenly divisible by 3, 27 is a multiple of 3.

Turns out, there’s a nice little trick for this as well. Add up the values of the digits. Is that sum a multiple of 3? If so, the number itself is also evenly divisible by 3. Check it out:

Is 543 divisible by 3?
5 + 4 + 3 = 12
12 is divisible by 3
So 543 is divisible by 3

Why does this work?

Place value is key here, but there’s an easy way to show your child what’s happening before you even introduce the trick. Do this with something tangible, like M&Ms or pieces of cereal.

  1. Start with 45 candies.
  2. Have your child divide the candies into two piles based on the place value—one pile of 40 candies and one pile of 5 candies.
  3. Now ask your child to divide the 40 candies into groups of 10 candies. (She should notice that there are four groups of 10 candies.)
  4. Now ask her this question, “How can you change each of these groups often, so that the number is divisible by 3?” She should suggest that you take away one candy from each pile. (If not, coax her to that answer.)
  5. Have her take one candy from each group of ten and move them into another group.
  6. Point out that she has six piles of candies: four piles of 9 candies, one pile of 4 candies and one pile of 5 candies.
  7. Ask her what happens if she combines the pile of 4 candies and the pile of 5 candies. She should notice that she’ll get 9, which is divisible by 3.
  8. By now, she will probably notice that the 4 and 5 come from number 45. See if she can come up with the trick, after doing this with a few examples using the candies.

So what do you think? Are math tricks a good idea or not? Do you have any other tricks to share? And can you explain why they work? If you need help with your math, I have written these great books to help you learn the easy way.

Categories
Math Education Math for Parents Math for Teachers

Lowering Homework Stress: 5 Easy Steps for Parents

Last week, I shared some unpopular opinions about homework. Mostly, here and on Facebook, people disagreed with me that three hours of meaningful homework was not too much. And looking back at that statement — which wasn’t exactly what I said — I see their point. Do I want my kid to be focused on academics for a full 10 hours a day? (Assuming that for those seven hours of school, she’s being taught.) When it’s put in those black-and-white terms, no, I don’t think that’s reasonable. Nor do I think the debate is all that black and white.

Regardless, parents all over the interwebs are pissed off about the amount of homework our kids are assigned. Their complaints range from the truly anguished (“I tried for two hours to help my son with his math homework, but with his learning differences, I just can’t get him to understand!”) to the kind of petty (“Having to sign a reading log is busy work — for me!”). It got me wondering, what do we do to lower this stress, for parents and students?

So I came up with some ideas. Try them out at home, and let me know how it works for you. And if you have your own ideas, please share them!

1. Reset the Priorities

What is the point of homework? Is it meant to help kids practice what they’ve learned? Extend lessons from class? Finish up something that didn’t get done in school? Complete a long-term project from start to finish? Torture you and your kid?

If you know what you want your kid to get out of homework, you can better set the parameters. See, this is your kid, not the school’s. What you want your kid to get out of his or her education matters. A lot. Once you know your homework philosophy, find out what the school and teachers think. (They might feel differently from one another.)

Then you’ve got to decide what hill to die on. If getting the right answer is a big deal for your kid’s math teacher but a conceptual understanding is what you value, someone’s going to have to compromise. For example, I’ve told my kid that I don’t believe timed math drills are useful tools. (And that’s backed up by research, y’all.) We agreed that if her grade was negatively affected by them, I would go in and talk to the teacher. Stress was instantly lowered. If signing a reading log is arduous for you, give your child that responsibility. Or decide that you’re not going to figure everything down to the minute and shoot for an estimate instead.

When the stress gets high, go back to those priorities. Talk to teachers about assignments that don’t meet your homework priorities. And if necessary, allow your kid to blow off things that are not meaningful. (Yes, I just said that.)

2. Set a Flexible Homework Routine

Whatever this schedule is, it needs to work with your family. Kids who go to aftercare may finish up their assignments before they get home. (At my daughter’s school, that’s a requirement for most assignments and students.) Other kids may come straight home, have a snack and shoot some hoops before hitting the books. Still others may not start homework until after dinner or even get up super early in the morning to finish an assignment.

Most kids really do count on structure, and it’s important that they know what to expect. At the same time, the schedule should be flexible enough to make room for everyday life — like a good cry after a fight with a friend or a quick trip to the ice cream shop for an after-school treat. When they know they can “break the rules” from time to time, they’re less likely to test their parents all of the time.

It’s also important to pay attention to how the schedule is working out — especially from year to year. My daughter used start her homework as soon as she walked in the door. But when she got a little older, it was apparent that she needed 30 minutes or so to unwind, to do something that had nothing to do with school. Of course, as kids enter middle and high school, this schedule should be their own.

3. STOP Reteaching

I can’t emphasize this enough. Stop it. Right. Now.

You are not the teacher. When you reteach, not only do you risk making your kid furious and even more frustrated with the work, you risk confusing your kid. Big time.

There is a reason that long division is going the way of the dodo bird. There is a reason that teachers introduce algebra in earlier grades. There is a reason that kids learn how to find the least common multiple before they learn to add fractions. And you might not know what those reasons are.

I would never attempt to perform brain surgery on my kid. I wouldn’t try to fix the hybrid system on my car. That’s because I’m not trained to do these things. And while many parents do an amazing job homeschooling their kids, mostly, they’re achieving this with the whole picture — and a lot of professionally developed resources.

This is probably the hardest step. It also holds the most promise for lowering stress. I promise.

4. Ask Questions, Don’t Give Answers

Want to know how to accomplish the last step? It’s pretty simple, actually. When your kid says, “I don’t know how to do this!” respond with a question.

“What does the assignment say?”
“Can you explain to me what the teacher asked for?”
“What is confusing you?”
“How can I help you figure it out?”

This puts the responsibility back onto your kid — where it belongs — without taking on any of her stress. Keep asking questions, even if she can’t answer them. Don’t solve the problems for her, but look for her to find her own solutions.

5. Let Your Kid Fail

Kids learn from making mistakes. We don’t do them any favors by preventing them from failure.

I’d rather my kid fail a homework assignment than a test and a test than a grade. And I’d rather my kid fail at something when she’s 10 years old than when she’s 40 years old. Failure at a young age won’t keep her from experiencing later failures. But she will learn from those little failures.

For that reason, you should quit checking your kids’ homework for accuracy. Heck, when they get to be in middle school, you should probably stop checking to see if their homework is done. Give them the right structure for success — space and time to complete homework assignments, little reminders, etc. — but let them chart their own way. (My friend and colleague, Denise Schipani calls this African-Violet Parenting. I call it parenting by benign neglect.)

So there you have it, five steps for lowering the homework stress in your house. I can’t promise that you’ll never have another fight with your kid, but I can say that following these steps will help you keep your cool.

Do you have other suggestions? Share them in the comments section. 

Categories
Math Education Math for Parents Math for Teachers

The Homework Wars: What matters? What doesn’t?

Last week, I heard from many friends and colleagues about Karl Taro Greenwood’s Atlantic.com piece, “My Daughter’s Homework Is Killing Me.”

“Amen!”

“I could have written this!”

“When are teachers going to learn that they’re piling on way too much???”

It was clear to me that the emotion of this piece resonated. But really what I think is this: Mr. Greenwood is probably a very nice man, but he comes off like a whiney, know-it-all parent. And he’s worried about the wrong damned things.

If you read Greenwood’s story, you know he’s worried that his daughter is getting too much homework. At the tender age of 13 years, she wasn’t able to fall asleep until after midnight, because of her homework load. He admitted that bias up front, and decided to see for himself. He took on his daughter’s assignments for a full week.

But really, what he should be paying attention to is the kind of homework his kids are doing.

At the same time, I can compeltely identify with his frustration about his kid’s bedtime. My kid often goes to sleep after midnight. She spends way too much time on homework, but I can say without hesitation that the fault lies with her, because her routine looks something like this: text friends, try to find her worksheet, text, check out when the new episodes of New Girl are coming on Netflix, text, do three math problems, text, find a new Pandora station on her phone, read her library book, finish her math, start science… well, you get the picture. By 10:00 p.m., she’s an anxious mess sometimes.

Her homework load is not too much. It’s generally between one and three hours each night, depending on how much she’s procrastinated on her weekly projects/assignments. (That is, if she actually gets to work, instead of goofing off.)

Greenwood’s daughter averages about three hours. Yes, that’s a lot. But if she’s staying up so late, it’s because she’s not getting started until 8:00 p.m.. (He never says why.) That’s a full five hours after my kid gets out of school, and even with her three-times-a-week soccer practice, it’s way, way later than she usually gets started.

But the thing that bothers me the most is what Greenwood writes here:

The Spanish, however, presents a completely different challenge. Here, Esmee shows me that we have to memorize the conjugations of the future tense of regular and irregular verbs, and she slides me a sheet with tener, tendré,tendrás, tendrá, tendremos, etc., multiplied by dozens of verbs. My daughter has done a commendable job memorizing the conjugations. But when I ask her what the verb tener means (“to have,” if I recall), she repeats, “Memorization, not rationalization.”

She doesn’t know what the words mean.

Shocking. Certainly, each subject requires a little bit of “fake it ’til you make it,” but not to know what the verb means is pretty amazing. And the fact that his daughter has so completely internalized the message “memorization, not rationalization” is truly tragic. That message goes against any educational philosophy I was taught at university.

At the same time, the author is incredibly proud of his (and his daughter’s) ability to pick up on the patterns presented by combining like terms in algebraic expressions. He whizzes right through those problems (none of the math homework is excessive, in my opinion), but has he merely memorized or is he really understanding what the process means? I could be wrong, but my guess is that he might have trouble explaining why the process works.

In other words, critical thinking is important in Spanish, science and literature, but really thinking through the whys of math? Nah, it’s way better to finish those problems as quickly as possible.

Easy homework = good homework?

The homework wars will never end. And that’s because when we all get home from work and school, no one wants the fight that ensues. We want to play board games or curl up on the couch and watch stupid television or read books that weren’t assigned to us.

But if teachers assigned homework that really mattered, would parents still be upset? If teachers asked kids to answer the hard questions, like “How did you get your answer?” or “Ask a family relative about his or her experience with immigration,” would we revolt, because that’s hard too? When schools are serious about rigor, do parents retaliate?

Homework shouldn’t be busy work. But I still believe that there’s real value to asking students to practice what they’ve learned or make some connections on their own. When we parents approach this in a positive way, we have an opportunity to teach our children than learning doesn’t stop at 2:50 p.m. or when we graduate from college.

What would happen if we sent our kids a positive message about their homework? (While working against excessive or stupid assignments, of course.)

This afternoon, my kid walked home from soccer practice, grabbed a snack and ran up to her room shouting, “I’m going to work on my science essay!” I don’t think this thing is due  until the beginning of next month. I didn’t have anything to do with her being excited to get to work. I also didn’t get in her way. She likes this assignment — probably because it’s challenging — and she’s happy to do it.

I’d say that one step in that direction is a little less whining, and a little more listening to kids and teachers.

P.S. Greenwood had lots of reasons to be ticked off about his kid’s school, starting with the lousy parent-teacher conferences. I don’t mean to suggest that he was off-base with everything.

P.P.S. Atlantic also had a great piece from a teacher, who is reassessing her practice of giving homework. I thought her reasons and concerns were compelling. Parents should read that piece as well: Should I Stop Assigning Homework? by Jessica Lahey.

What do you think about the homework your kid is getting? Homeschooling parents, what’s your take on the homework wars?

Categories
Math for Parents Math for Teachers Math for Writers Math Secrets

For the Love of Math

Last Friday, my family adopted a sweet, little poodle puppy, named Zipper. The foster mother, Sally, had brought him from a Mexico shelter to her own home in Silver Springs, Md. During the home visit on Friday, we talked about our careers, and I mentioned that I write about math. That’s when she told me about her neighbor, the mathematician and novelist.

“You two should meet!” she said. Apparently, we have some of the same ideas about math.

Well, I did “meet” Manil Suri today, via the pages of the New York Times op-ed section. His excellent piece, “How to Fall in Love with Math” points out some ideas I’ve been extolling for years — along with a couple that I might have said were hogwash a couple of weeks ago.

As a mathematician, I can attest that my field is really about ideas above anything else. Ideas that inform our existence, that permeate our universe and beyond, that can surprise and enthrall.

Yes, yes, and again I say, yes! Mathematics is not exclusively about numbers. Hell, arithmetic is only a teeny-tiny fraction of what mathematics really is. Mathematics is the language of science. It’s a set of systems that allow us to categorize things, so that we can better understand the world around us.

Math is a philosophy, which I guess is what makes us math geeks really different from the folks who are merely satisfied with knowing how to reconcile their accounting systems or calculate the mileage they’re getting in their car. We mathy folks are truly interested in the ideas behind math — not just the numbers.

Last week, I attended a marketing intensive, a workshop during which I outlined my current career and explored how I want to take things to the next level. I’m ready to think bigger, and I need a plan to get me there.

The other entrepreneurs there thought there was real value in my creating a coaching service for entrepreneurs. My services would center around the numbers that these folks need to make their businesses survive and thrive. Marketing numbers, sales numbers, accounting numbers. They resisted the word “math” and advised me to really underscore the numbers.

From a purely marketing standpoint, I completely get it. I don’t have so much of a math wedgie that I can’t understand that the word “numbers” may be less threatening than “math.” So why not just go for it?

But the entire process left me thinking about what it is that draws me to mathematics. And ultimately what will drive me in a career, what moves me to get up in the morning and say, “Let’s go!” If you’ve been around here long, you know that it ain’t the numbers, sisters and brothers.

At the same time, I can’t say that I love math. But maybe that’s semantics, too. For the last two years, I’ve said that I’m attracted to how people process mathematics. But isn’t that just philosophy? So, isn’t that just math? This is what Suri had to say:

Despite what most people suppose, many profound mathematical ideas don’t require advanced skills to appreciate. One can develop a fairly good understanding of the power and elegance of calculus, say, without actually being able to use it to solve scientific or engineering problems.

Think of it this way: you can appreciate art without acquiring the ability to paint, or enjoy a symphony without being able to read music. Math also deserves to be enjoyed for its own sake, without being constantly subjected to the question, “When will I use this?”

At first, I disagreed with Suri’s thesis that math is worth loving — for math’s sake alone. But his analogy here is right on target. I couldn’t paint my way out of a paper bag, but each and every time I see “Starry, Starry Night” at MOMA, I catch my breath.

We come back to a failure to educate, as Suri so wonderfully elucidates in his piece. When we allow people who hate — or don’t appreciate — math to teach the subject, well, does anyone think that’s a good plan?

At any rate, I hope you’ll take a look at Suri’s piece. Meantime, I’m going to reach out to him to share my appreciation of math. Maybe there is a way — beyond teaching — for me to make a living as a math evangelist.

What do you think? Do you notice a difference between mathematics and numbers? Have you changed your mind about math in recent years or month? Please share!

Categories
Math for Grownups Math for Writers

How This Book Editor Learned to Like Math

Behind every author is a great editor. And I was dang lucky to have Jennifer Lawler as my editor for Math for Grownups. What I didn’t know was that I’d helped her out, too. Who says English majors can’t do math? Here’s her story:

A few years ago, I was working as a book development editor for Adams Media, the company that published Laura’s Math for Grownups, and I was assigned to edit the book. While I was looking forward to working with Laura, I was also a little nervous. Although I’m pretty good with basic math operations, I’m not that confident and tend to second-guess myself a lot. I just hoped that when I asked Laura questions that she wouldn’t give the dramatic sigh that my seventh-grade algebra teacher used to do when I expressed confusion.

Fortunately, she didn’t. Laura, like her book, is a kind and supportive person. It was fun to see that aspect of her personality show up on the page. And it was a project that helped me learn more about math than I did in junior high and high school combined. I don’t mean I memorized a bunch of formulas. I mean I learned a new way to think about math.

One of the first things Laura discussed in her book was the various ways people use to arrive at an answer to a problem. For years, I’d felt like I was doing math wrong, even though I was getting the correct answer, because I had a bunch of little shortcuts and methods I used that I had never been taught by a teacher in school. Laura showed how that is just fine—and she also emphasized the point that often in life we don’t need to be exact, we just need to be reasonably close. We can estimate, another habit I have that I always thought was somehow wrong of me to be using.

Because Math for Grownups was meant to be a review of  mathematical concepts for people just like me, I figured that any question I asked Laura was a question that a reader like me might have. So for the first time in my life, or at least since seventh grade, I didn’t feel embarrassed about asking math questions. “I’m doing it for the reader!” I told myself, and then Laura would either explain what I had missed or add a note or a sidebar to address the question. As the process continued, I felt more and more confident about my abilities. And I stopped beating myself up for making a mistake. Do I agonize over a typo in an email I dash off to a friend? No, because I know I’m a good writer and so I don’t feel defensive about it. But I used to beat myself up for simple math mistakes that anyone can make. That just made me feel even worse about math.

Laura pointed out that even mathematicians make mistakes in simple computations. For some reason, I hadn’t made that connection before. If I, a professional writer, can make a spelling error in an email, then of course even a mathematician can sometimes multiply 9 x 9 and come up with 72.

One of the things that working with Laura taught me was to ask myself questions about my results in order to catch those simple mistakes—questions along the lines of, “Does this answer seem reasonable?” So, if I’m doubling a recipe, and my calculation for the double batch shows an amount smaller than for the single batch, I know I’ve done something wrong. This is the math equivalent of proofreading, and once I understood how it worked, I was a lot more confident about my answers.

By the same token, I learned that I could look it up, just the way I do for a word I can’t remember how to spell. There’s nothing shameful about not remembering the formula for calculating volume. And I’ve dog-eared many pages in Laura’s book where I can find formulas I use a lot but can never seem to remember. I can never remember how to spell “occasionally” (have to look it up every.single.time) but I don’t think that somehow makes me a bad writer. Working with Laura taught me how to apply this same type of thinking to my math skills.

My greatest reward? Now I deal with math like a grownup, instead of like that frustrated seventh-grader I once was.

Jennifer Lawler is the author or coauthor of more than thirty nonfiction books as well as sixteen romances under various pen names. Her publishing experience includes stints as a a literary agent and as an acquisitions editor. She just released the second edition of Dojo Wisdom for Writers, the second book in her popular Dojo Wisdom series. She also offers classes in writing book proposals, planning a nonfiction book for self-publishing authors, and writing queries and synopses for novelists at www.BeYourOwnBookDoctor.com (under the “classes” tab).

And have you heard? I’m working on a new ebook, Math for Writers. Stay tuned for details!

Categories
Math Education Math for Parents Math for Teachers

Dear Math Teacher

I’ve been talking with grownups about math for more than three years now. Parents, 20-somethings, writers, DIYers, seniors… they all have something in common: a piss-poor relationship with math.

This bad attitude is probably your fault.

The stories I hear — over and over and over again — all point to a major breakdown in the educational system. Sure, we can blame standardized testing or the state standards themselves. Middle school teachers can blame elementary school teachers. High school teachers can blame middle school teachers. College professors can blame high school teachers. And by all means, let’s not leave out the parents.

But you, dear math teacher, have control over only one thing: yourself. So what are you going to do about it? Here are some ideas.

Be Nice

If I hear one more math teacher opining about how dumb his students are, I think I might scream. Why do people teach, if they don’t like their students enough to be nice to them? Your students aren’t dumb. They’re uneducated. And guess whose job it is to educate them? If they come to your class unprepared, tough noogies. You get the kids you get. You were hired to overcome those obstacles. That’s the job, and if you can’t deal with it, perhaps this isn’t the right profession for you.

Don’ take your frustrations out on your students. Quit talking down to them. Quit berating them in public. Quit rolling your eyes or slamming doors. Be a grownup. They’re kids, and they respond to kindness and respect. Give it to them, and you’ll likely see motivation.

Inspire

You don’t have to be Martin Luther King, Jr. or Oprah. But lose the this-is-good-for-you-so-do-what-I-say attitude. It doesn’t work.

Look, you teach math for some important, personal reason. What is it that motivates you? Dig deep, find that thing, and share it with your students. Go for that spark every single day. It’ll make you feel better and get your students motivated.

It’ll also make your job MUCH easier. An inspired kid will work, will stop playing around when you ask her to, will make deeper connections. An inspired kid will meet you halfway. This gives you more energy to devote to that kid who is still messing around in the back of the room or who is ready for the next unit before the rest of the class. Inspiration means autonomous learning.

Teach Students, Not Math

Wait, did you actually think you were going to teach math? Sorry, but that’s not the job. Math teachers don’t get to immerse themselves in math all day long. Nope, your job is to teach kids. Whiny, pain-in-the-butt kids who are more interested in last night’s episode of Pretty Little Liars than their upcoming geometry test. BECAUSE THEY’RE KIDS!

Whether you like it or not, most of your students don’t give a flying flip what x is. Most adults don’t care either. You want your students to learn math? Recognize each and every student as a person, not a container to be filled with math facts. Let them experience the subject for themselves. Let them teach you.

The most effective teachers have students who will follow them to the ends of the earth. And that’s no accident. Students of all ages can spot a bullshitter in two seconds flat. They yearn for genuine relationships with adults. You give them that when you recognize that math isn’t the be-all-end-all of their day. You give them that when you see them as a whole person, not just a math student.

Be Real, But Not Too Real

Having a bad day? Own it. Frustrated with how things are going? Take responsibility. All classrooms — even the most traditional — are two-way streets. When you are real with your students, they’ll be real with you.

But expect to get some pretty raw stuff in return. Kids can’t act like adults, because — guess what? — they aren’t gown up yet. You’re modeling for them every, single day what it’s like to be a grownup. When you react to their realness with childish behavior, well, that’s a pretty strong message.

And for goodness sakes, draw some lines. Sure, you hate standardized testing. (What teacher doesn’t?) But really, do you need to share that ad nauseam with your students? Heck, you might have tremendous disdain for how administrators are running the place, but keep your trap shut on that subject. These kids aren’t your friends. And again — they’re not grownups.

Notice something? There’s not a single number, mathematical concept or teaching strategy in the above advice. I really believe this from the bottom of my heart: It’s not about the math. It’s about how you relate to your students. Every.single.time. You have way, way more power than you can even fathom. Your students carry the messages you send to them — throughout their lives. Try it. Ask five friends about their math education. I guarantee that four of them will have detailed, sad stories about why they hate math.

You have a chance to turn this around for thousands of students. And honestly, if you’re not up to the task, get out of the freaking way. Let someone else do it. Because you can do a hell of a lot more damage to one student than a kid could ever do to you.

Sincerely,

Laura Laing (informal therapist to math-haters of all ages)

Categories
Math for Grownups Statistics

Math and Cancer and Feelings: Or, where the heck have I been?

No. I do not have cancer. But in April and May and June of this year, I thought I might.

So that’s the answer to the question in my headline. I’ve been taking a break while I deal with the roller coaster of emotions that come with suspicious mammogram and biopsy results and then surgery. First, the story.

In April, I had an ordinary, run-of-the-mill mammogram. I’m what you call a non-compliant patient, and so I’ve only had one other mammogram in my life. Turns out both of these great experiences ended up with biopsies. My first feeling was to be totally pissed off. I’d had a biopsy before, and let me tell you, they are not fun. And since the first one showed nothing, I expected that this would be more of the same — an exceedingly uncomfortable and nerve-wracking experience that showed nothing.

Except it didn’t. The biopsy showed “atypical” cells. This means I had something called Atypical Ductal Hyperplasia or ADH. This is not cancer. These atypical cells cannot even be called precancerous cells. My amazing surgeon explained: Research shows that women with ADH have an increased chance of those atypical cells becoming cancer. Here are the numbers:

  • Women without ADH have about a 5 percent chance of getting breast cancer.
  • Women with ADH have a 20 percent chance of getting breast cancer.
  • And that means women with ADH have four times the chance of getting breast cancer.

For me, those numbers pointed to a very easy decision: to have the area with ADH removed. On July 5, I had a lumpectomy. Then I waited for the pathology results. I waited for 10 days.

Anyone who has gone through something similar knows the special hell these ten days were. I am not a particularly emotional person. And yet, these ten days were downright terrifying. And here’s why.

There was a 20 percent chance that the lumpectomy would reveal cancer. In other words, there was a slight chance that the biopsy missed any cancerous cells that were already there. Of course, that meant I had an 80 percent chance of no cancer at all.

After the surgery, I updated my friends and family. One physician friend emailed me back: “I hope you find some solace in those stats (ie the 80%).” I assured her that I did. (No lie at that point.) And she followed up with this:

“Glad to hear how you’re taking it. You are right about the stats.  They are often very difficult for patients, because if there is a small chance of something, but a patient has it, that patient has 100% chance of having it, right? But we as physicians use stats all the time, especially in the office setting where you don’t have any and every diagnostic test at your fingertips, and with the cost– psychological and financial– to the patient: what is the chance that this patient with this headache and those symptoms has a brain tumor? What are the chances that this person’s chest pain is a heart attack and not indigestion? It is probability, given symptoms, age, and a slew of other factors, in combination with the implications of a given diagnosis.”

These numbers were supposed to ease my mind. Except feelings + stats + time = complete and utter freak out.

By day nine of my waiting period, I was a total wreck. I cried all day long. I wasn’t sure if I was going to be able to sleep. I was nervous as a long-tailed cat in a room full of rocking chairs.

Happy ending: I don’t have cancer. I know that not everyone gets that amazing news, and I am extremely grateful. I am being followed very closely, because my chances of getting breast cancer are still higher than most women’s. And I’m taking tamoxifen for the next five years, which reduces my chances by half. Those aren’t bad stats either.

I never thought that math was the be all end all, but I have often railed against misinterpreting numbers to incite fears and advocated for the use of statistics to ease worry. Still, feelings don’t always play well with math, I’ve found. When a person is worried — scared, even — a pretty percentage may not be comforting. And that’s okay, too. We all do the best we can with what we’ve got.

What’s your story with health and statistics? Has a percentage ever frightened you to the point of distraction or temporary insanity? Share your story here. You are not alone!

Categories
Math at Work Monday

Math at Work Monday: Chappy the fitness coach

Raise your hand if you’re trying to get in shape for swimsuit season or a wedding? (I’m raising my hand!) May is prime time for folks to either get more serious about fitness or fall off the wagon. But fitness coaches like Chappy Callanta can help us stay focused to the very end — and then keep toned and slender. His gym in the Phillippines, 360 Fitness Club, not only offers expertise but equipment and classes, too. And — you guessed it — Chappy uses math. Here’s how.

Can you explain what you do for a living?

I develop strength and conditioning as well as general fitness programs for my gym. It involves a lot of research, a lot of experimentation and of course a lot of exercise. I also train teams and personal clients. I help them lose weight, get stronger, achieve a specific goal like running a marathon or even manage special conditions. I also write for Yahoo Philippines as their resident fitness blogger, and I maintain my own blog. My passion is fitness and wellness, and my mission is to spread the good word of being healthy to as many people as I can.

When do you use basic math in your job?

All the time actually. I use math when we compute for ideal weights of clients, find the right training load, or determine the number of calories one needs to consume to achieve a weight loss goal. I use math whenever I design programs for my clients. One specific situation when I use simple math would be when dealing with a weight loss client. One pound of fat is 3,500 calories. If you want to lose weight at a rate of 1 pound of week (which is doable and not too hard), you will have to create a deficit of 3,500 calories per week. I present this to a client and break down how she will be able to do it. We divide it by 7 because there’s 7 days in a week. Then we divide it by 2 because you want to lose weight through exercise and diet. That leaves you with 250 calories that you have to lose via exercise, and 250 calories through your diet. We’re just subtracting 250 calories per day from her regular diet and adding 250 calories worth of exercise per day. We compute for this using the MET system (metabolic equivalent of tasks) which takes into account the weight of a person and multiply it to the corresponding MET value of a specific activity.

Calories Burned ÷ hour = Weight in KG • MET value

For example, I weigh 80kg. The MET value for jumping rope is 10Mets. So if I skip rope for 1 hour I will lose 800 calories. That means if I want to lose 250 calories, the equation is:

Time = 250 cal ÷ (800 cal ÷ 60) = 18.75 minutes

Do you use any technology (like calculators or computers) to help with this math?

I usually don’t since I’m so used to it already. I write it down though on paper while I’m computing it so my clients see how the math works.

How do you think math helps you do your job better?

It helps me to explain how the body works and how easy it is to lose or gain weight by using basic math and applying it to food and exercise. I believe that every trainer should practice mental math, so it’s easier to compute for the right training volume and intensity, as well as using the right load for each exercise.

How comfortable with math do you feel?

I’m relatively comfortable with basic math. There really isn’t much calculus involved in my line of work. Most of it is basic arithmetic and operations. Geometry is also important when analyzing sports and the optimal angles of the joints for a specific activity.  Research shows how the ankles, knees, and hips should be angled for example when diving off the high dive. It’s useful information and it’s pretty cool also.

What kind of math did you take in high school?

I took Algebra, Geometry, Trigonometry and Calculus. I enjoyed it until we got to calculus. My grades showed that I was good at it but I enjoyed Geometry the most.

Did you have to learn new skills in order to do the math you use in your job?

It was something that I already knew but I felt that I needed to practice it more. I practiced the equations and mental math with my clients so that today, I’m confident that I can do basic operations off the top of my head.

Do you have questions for Chappy? Feel free to ask in the comments section, and I’ll let him know. Also, take a look at his blog, which features great, inspirational tips. 

Categories
Math at Work Monday

Math at Work Monday: What I’ve learned

It’s been a long while since I’ve posted a new Math at Work Monday interview. But this feature remains one of the most popular here at Math for Grownups. Perhaps that’s because teachers and parents like to prove to their kids, “See, you will use this stuff one day!” And I imagine that others stumble upon it while looking for career advice. At any rate, it’s been an eye-opening experience for me, too. And here are a few lessons learned.

People don’t know they’re doing math

I’ve intentionally  focused on careers that are not traditionally STEM related — from a textile designerto an FBI profiler to a children’s book author. And almost everyone says the same thing: “I don’t use much math in my work.” Then they follow up with a revelation – they do more math than they think!

People do the math they want to do

This makes a lot of sense. Why go into a career that requires skills you don’t have? Those folks who really dislike calculus are most likely not going to become physicists. Folks who hate statistics avoid careers in research. And people who have a disdain for geometry aren’t likely to become carpenters or architects. At the same time, when someone feels drawn to a career, they’re willing to whatever it takes to be successful. That often includes a little bit of math.

People do a lot of mental math

While most folks I interview say that they check their work with a calculator or good old back-of-the-envelope calculations, a fair amount of math is being done in their heads. This may be as simple as using fractions to mix the perfect hair color to deconstructing formulas so that the math can be done in the field, say on a fish hatchery.

People also depend on technology

When it comes to money, especially, or critical situations, like healthcare, a computer, spreadsheet or calculator is often a necessary tool. But often these require a clear understanding of the math going on. It’s not enough to give someone some software. These folks must know how the math works in order to use their technological tools.

People often don’t have a good relationship with math

This is kind of sad to me, but it’s been very true: I rarely meet someone in a non-STEM field who says that they really understood math in school and now feel really confident in their skills. Yet, all of the folks I interview for Math at Work Monday do use math. That says to me that their issues with math are often in their head – and probably not really their fault. The reality is that our educational system and other adults often fail us in this regard. It’s not about making math fun. It’s about making math useful.

I’d like to keep Math at Work Monday going, but I need your help. Do you know someone who would be interested in being interviewed? Think of basic fields: home improvement, medicine, the arts, law, public service and more. Does your partner use math in his work? What about your next door neighbor or your sister? The answer is yes, and I’d like to interview them. Shoot me a line at llaing [at] comcast [dot] net, and I’ll reach out to them.

What have you learned from the Math at Work series? Have you been surprised by anything? Share your thoughts in the comments section.

P.S. I wanted to explain why I was so silent last week. Because of the horrific events in the U.S., I felt it would be trite to post about Math Awareness. Clearly our national attention was needed elsewhere, and so aside from a Boston-related post, I made the decision not to post. My thoughts continue to be with everyone in Boston and West, Texas.

Categories
Math Education Math for Grownups Math for Parents Math for Teachers Math for Writers

Getting Aware of Common Core Standards

Not all of us are parents or teachers, but I’ve long asserted that education is a “public good,” something that each and every one of us should be very, very concerned with. When kids don’t graduate or graduate with poor critical thinking skills, a lack of curiosity of the world around them or a dearth of basic math, reading and writing abilities, everyone suffers. And in a world where STEM-based employers are recruiting and paying more, we owe it to the next generation to do better.

(This is not to say that our educational system doesn’t have some absolutely enormous issues in other areas. Perhaps the biggest problems our schools face are not academic at all. I believe that if our country took a good, hard look at poverty, violence and teacher care, we’d make huge strides in the right direction. But this post is about academics.)

Enter the Common Core Standards. For decades, each state has developed and cultivated its own standards – or objectives required by each basic course, from history to language arts to biology. But over the last 20 years, a movement has grown to standardize these objectives across the country. With this umbrella of standards, what little Johnny is learning in Arkansas will be similar to what little Patrice is learning in Maine.

Right now, the Common Core Standards only cover English (language arts) and math. They’ve been adopted by 45 states. (Alaska, Nebraska, Texas and Virginia haven’t adopted them at all, and Minnesota adopted only the English language arts standards.) Standards for other subjects are in the works, including science and social studies.

For the last six months, I’ve been writing and editing curricula designed to meet the Common Core Standards for mathematics. I’ve gotten a pretty good feel for what they are, and I have to say that I like them for the most part. Here are some general thoughts I have:

Students will learn certain concepts earlier. I haven’t spent much time with the elementary level standards, but at least in middle and high school, various mathematical topics will be introduced earlier in the standards. For example, exponential functions (an equation with x as an exponent, like with exponential decay or compound interest) is covered in Algebra I, rather than Algebra II. 

The result is two-fold. As the standards are rolled out, some students will be left behind. In other words, kids who started school without Common Core may have a hard time catching up or bridging the gap. Second, students will have the opportunity to learn more mathematics throughout their high school career. The idea is to better prepare them for STEM in college and careers.

The emphasis is on critical thinking. This part, I love, love, love. For example: geometry proofs are back! And rather than compartmentalizing the various branches of mathematics, students will make connections between them. I just wrote a lesson that looks at how the graphs, equations and tables for various functions – linear, quadratic and exponential – are alike and dissimilar. Previously, students may never have seen these functions together in the same unit, much less the same lesson.

This means that assessments will change. Students will be asked to explain their answers or verbalize the concepts. Expect to see much more writing and discussion in math class.

Applications, applications  applications. Math is no longer done for math’s sake. And this couldn’t be better news. As I’ve said here many times before, math is pointless until it’s applied. Students should get this first-hand with Common Core, which outlines very specific applications for various concepts.

The idea here is to demonstrate that the math they’re learning is useful. The result? Hopefully more students will choose to enter STEM careers or major in these fields in college.

Students learn in different ways. Modeling plays a big role in the new standards, which means that students can approach the math in a variety of ways – from visualizing the concepts to using manipulatives like algebra tiles to working out equations in more traditional ways to graphing. This way, students can enter the material from a variety of different doors. And that can translate to greater success.

Sure, there is a lot to be concerned about (most especially the gap that we expect to see in student performance), but from my perspective the Common Core Math Standards are a step in the right direction. It’s important to know that these do not form a federal curriculum; the states are still responsible for choosing curricula that meet these standards, and education resource companies are scrambling to meet these meets. (That means I’m very, very busy these days!) It’s also important to know that chucking old ideas and implementing new ones puts a huge burden on already over-taxed schools and school systems. Finally, there is no doubt that this initiative was driven by the textbook companies, which means we’re still beholden to politics and capitalism.

But in looking at the standards alone, I think Common Core is excellent. If we can implement the standards well and keep them in place for a while, I think our kids will benefit.

What do you think of Common Core? Share your thoughts in the comment section.

Categories
Health Math for Grownups Math for Parents

Another Awareness: Organ donations

KONICA MINOLTA DIGITAL CAMERA

Math shares its awareness month with another mission that is very near and dear to my heart: It is also Organ Donor Awareness Month. When I found that out earlier this week, I thought I’d indulge myself a bit and spend a post looking at the math of organ donation.

When I was in middle school, my father learned that he had a very strange autoimmune disorder. His immune system was attacking his liver. In fact, his liver looked like that of a raging alcoholic, which he wasn’t. After months and months of testing and treatments (some pretty ugly), his doctors were finally able to get things under control. But they told us one thing that stuck with me forever: “This isn’t a terminal disease, but it is chronic. As a result, he won’t live as long as he would have if he was healthy.”

To this day, we have absolutely no clue why my father’s immune system turned on him. When I was a toddler, he had surgery to remove part of his thyroid, because it was so overactive. As he aged, he developed other autoimmune disorders, including vitiligo, which caused his skin to lose pigment. But he kept on keeping on.

About seven years ago, his doctors discovered liver cancer. This was a specific kind of cancer, related to his liver disease. They could remove it, but the writing was on the wall: his liver was on its last legs.

So they put him on the liver transplant list. He stopped travelling more than a couple of hours from his hospital. He got poked and prodded. And he waited. And waited.

I’m not sure how many people were on the list at the time. Today, there are nearly 17,000 people waiting for liver donations. Each of these individuals are scored, based on the severity of their liver damage. In 2006, when my father was on the list, the median national waiting time was 321 days. I wasn’t able to find out how many people die before receiving a liver transplant, but it’s estimated that 6,500 people die each year while waiting for a heart, kidney or liver.

After eight months or so of waiting, my family and his doctors got worried. The tumors were coming back and multiplying. He needed a transplant soon. And so I made a decision that changed my life forever. I would donate my liver to him.

The liver is the only organ (besides the skin) that grows back. And a live-donor liver was a great option for someone like my dad. I flew through the medical testing with flying colors.

At about 5:00 a.m. on October 1, 2007, I was wheeled into an operating room at Virginia Commonwealth University Medical Center. They prepped me first, and then brought my father in for the transplant. The entire surgery took at least 8 hours, during which they took one full lobe of my liver and transplanted it into my father. Something like two hours of that time was devoted only to stitching up the large lambda-shaped incision that cut through my abdomen.

After two days of recovery, my father was off the ventilator, and I was walking down the hospital corridors on my own to visit him. Within another two weeks, an MRI showed that my liver had already grown back to about 95% of its original size. (I’m not kidding!) In that time, I had lost around 20 pounds, from not being able to eat for about a week and from the energy my body spent regrowing an organ.

I’m so sad to say that this story does not have a happy ending. I’m perfectly healthy. And my transplanted liver was doing great inside my dad. But no one knew that my father had pulmonary fibrosis. It must have been at the very, very early stages of his disease when he was tested and tested and tested prior to the transplant surgery. The doctors suspect that the progression of the disease was sped up considerably due to massive amounts of oxygen that were pumped into his lungs during surgery and while he was in intensive care.

Had he not had this complication, I have no doubt that he would be living today. He died on November 6, 2007; his liver was still going strong.

My point is not to share a very sad story. My point is to share with everyone some small mathematical facts about organ donation:

1. Each day, about 18 people die, while waiting for a kidney, liver or heart. (That’s 6,500* people per year divided by 365 days.)

2. Right now there are approximately 117,729 people waiting for a kidney, liver or heart. Each year, 4,000 more people join this list.

3. Becoming an organ donor doesn’t have to be as dramatic as my experience was. Most donated organs are from a deceased donor. It takes a split second for you to indicate on your driver’s license that you want to be an organ donor. Or you can sign up at OrganDonor.gov.

4. And happily, most people do not have my father’s experience. As of May 2009, 73.8% of those who had received a transplanted liver were still alive, five years after their surgery. Here are the percentages for others: 69.3% of kidney recipients, 74.9% of heart recipients and 54.4% of lung recipients.

5. It’s not just the big organs that matter. Organs and tissues from a single deceased donor can help up to 50 people. (Yes, 50!) On average 79 people each day receive a donor organ or tissue.

In fact, my father was so convinced of the value of organ donation that even after much of his body failed him, my father was able to donate his eyes, skin and tissue. It is an amazing thought that I and he were able to join together to do this.

So if you haven’t taken the time to indicate that you’d like to donate your organs after death, please do so now. I don’t regret for a moment my gift to my father. At the same time, had there been more deceased donors, it wouldn’t have been necessary.

Talk to your family about organ donation. Get some good information. And at the very least, make an intentional decision one way or the other.

*Earlier, I had a typo here. This number has been corrected.