Welcome to Day 1 of our tour of basic math. If your New Year’s Resolution is to brush up on your math skills. You’re in the right place.
Winter is really the perfect time to talk about integers.
But first, what are integers? It’s quite simple, really. They’re positive and negative whole numbers. These are integers: -547, 9, 783, and -1. These are not integers: 0.034, -0.034, √3, and -1/2.
You are very familiar with positive integers. For the first three years of your formal education, you probably worked exclusively with these little buggers — or as you called them, “numbers.” You learned to count them, tell time with them, add/subtract/multiply/divide them, and even write them out as words.
(Soon after, you learned about fractions and then decimals, which are not integers, but are still positive, so it was all good.)
If you’re like me, the part that completely blew your mind was when you first learned that numbers could be negative. Now that I think back, this was kind of a silly surprise in my world. I grew up in an area of the United States that gets pretty cold in the winter. This means two things: we measured temperatures with Fahrenheit and the temps got below zero. And those two things pointed to negative numbers. Duh.
Regardless, with a lot of work and determination, I finally understood integers, which included adding and subtracting negative and positive whole numbers. But before I show you how this is done, let’s take a look at the number line, which can help you visualize how this works.
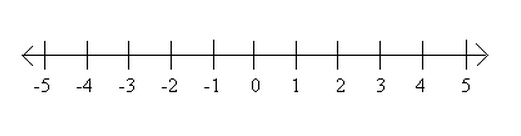
The number line isn’t a real thing. It’s just a way to visualize how numbers work. And the key is the zero in the middle of the line. Notice what happens on the right — the numbers get larger, one by one, right? And what happens on the left? Yep, they get smaller.
Did you get that smaller part? If not, don’t worry. You’re just a little rusty. See, when two numbers are negative, the smaller one actually has the larger numeral. In other words -37 is smaller than -1, while 1 is smaller than 37.
(This is a good time to note something else that you may have forgotten. If a number has no sign, it is positive. The positive sign, +, is understood.)
If you can picture a number line, you can add and subtract integers, no problem. Here’s how:
-1 + 3 = ?
Start at -1 and count three places to the right. We’re counting to the right because we’re adding. What is the number on the number line? If you said 2, you’re right on target.
4 – 5 = ?
This time start at 4 and count five places to the left. That’s because we’re subtracting. What do you get? If you said -1, give yourself a gold star.
So this number line thingy is pretty cool, but it’s not all that useful if you need to find an answer pretty quickly. And what happens if the second number is negative? (Well, you change direction, actually, but that’s pretty clunky and somewhat confusing. So how about if we find another process?)
Once you understand the why of adding and subtracting integers, you can learn an algorithm that works every single time. It goes like this:
This is much easier to understand with an example:
-10 + 4 = ?
We’re adding two numbers with different signs. That means we need to ignore the signs, find the difference and take the sign of the larger numeral. But what does “find the difference” mean? It’s pretty simple, actually. Just subtract the smaller number (without the sign) from the larger number (without the sign). 10 – 4 is 6, and if we take the sign of the larger numeral, the answer is -6.
Another way to think of “difference” is the distance between the two numbers on the number line. So if you got back to the number line, it’s a matter of counting spaces between the two numbers. Then take the sign of the larger numeral. Make sense?
-10 + 4 = -6
Okay, let’s try a subtraction example.
-3 – 9 = ?
First step is to change the subtraction to addition and change the sign of the second number.
-3 + -9 = ?
Now all you need to do is follow the addition rule for numbers with the same signs. That means to ignore the signs, add, and keep the sign.
-3 + -9 = -12
So, no need to pull out a number line for these. Just practice with these rules, and you’ll have them down in no time at all. Here are a few additional examples to help you.
5 – 8 = 5 + -8 = -3
-7 – 4 = -7 + -4 = -11
3 + -3 = 0
-12 + 8 = -4
Now, try these out on your own. I’ll post the correct answers on Friday. And if you have questions, ask them in the comments section.
1. 15 – 25 = ?
2. -7 – -3 = ?
3. 10 + – 8 = ?
4. -3 – 12 = ?
5. -6 + 4 = ?