Parks and Recreation, the Amy Poeler-driven mocumentary on NBC about a small-town parks department, features a tightly wound character, Chris Traeger, whose favorite word is literally – as in: “Biking for charity is literally one of my interests on Facebook.” It’s funny because it makes us grammar fanatics crazy. Literally is literally one of the most misused and/or overused words in the U.S.
I had never seen the word applied to mathematics until recently. No kidding! That’s when I learned about literal equations. I mean, I already knew about them; I just didn’t know what they were called. And yes, you know about them too. They’re one of the ways that we use algebra in our everyday lives – without even knowing it.
Literal equations are equations with more than one variable. Ta-da! See, you knew about them, too. Here are some examples, in case you’re not convinced:

Look at all of those variables. Each equation has more than one, which means that each of the above is a literal equation. That’s it. Easy.
Now, the algebra of literal equations is much, much easier than most mathematics, especially if the equation is simple, like the distance formula. (Don’t panic. This is not one of those train-leaving-Pasadena questions.) The algebra is in identifying the variables, substituting into the equation and then solving.
Let’s say that you’re an avid cyclist. In fact, you’ve got all the cool accouterments, like a gel-padded seat, clip-on pedals and a speedometer. You average about 16 miles per hour on flat roads, and you love trying out new routes, just riding where your bike takes you. But it’s critical that you know the half-way mark for most of your routes – otherwise, you won’t have enough steam to get back home.
That’s where the distance formula can come in. If you know your speed (or rate, r) and the time you’ve been out, you can find the distance. This way, you know when to turn around and head back to enjoy those endorphins.
One gorgeous Saturday morning in March, you head out on an unfamiliar route, cruising at about 16 miles per hour. Checking your watch, you find that you’ve been on your bike for half an hour. How far have you traveled? You can actually do this math in your head – just multiply 16 by 0.5. How do I know this? With the literal equation d = rt.
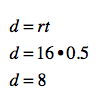
See? You just used a literal equation. And you did it on your bike. As Chris Traeger would say, “You are literally the most impressive cyclist I know.”
How have you used literal equations recently? Want to share in the comments section? Feel free. Also, feel free to challenge my thesis that algebra is an important part of a solid middle and high school education. I can take it. Really.
