Welcome to Week 2 of January’s Back to Math Basics — a quick review of the basic math that you need to do everyday math. Answers to last Friday’s integers questions are at the end of this post.
When kids are first learning about fractions, teachers often turn to something that all but the lactose- or gluten-intolerant can appreciate — pizza! (And I can empathize with the allergy inclined. For you, imagine a dairy-free, vegetable pie with polenta crust — yum!)
This is for very good reason: Fractions are simply parts of the whole. When you cut a pizza into 12 equal parts you are creating twelfths. To count them, you’d start at one piece and count around the pizza (or in random order, makes no diff): one-twelfth (1/12), two-twelfths (2/12), three-twelfths (3/12)… all the way to 12-twelfths (12/12) or the whole pizza (1). Half of the pizza is six-twelfths (6/12) or one-half (1/2). A fourth of the pizza is three-twelfths (3/12) or one-fourth (1/4). Get it?
(Okay, so it’s really, really hard to write a blog post about fractions. In Word, I can depend on something call MathType to write fractions, which I’ll create for examples below. But in paragraphs, this doesn’t work so well. So please bear with me!)
It might make sense to start with addition and subtraction, but in this case, multiplication and division is the better start. (Spoiler alert: You’ll use multiplication to add and subtract. Really.) But just like with integers, multiplying and dividing fractions are really, really easy.
So let’s go back to those pizzas. Let’s say your son is having a birthday party, and he wants to serve pizza. If each kid can eat 1/4 of a pizza and there are 12 kids at the party, how many pizzas do you need to buy? (Seriously, this is not as dorky a question as it might sound. I have had to figure this out IRL.)
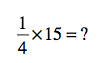
Are you actually multiplying two fractions here? Why, yes. Yes you are! In fact, any whole number can be written as a fraction — just use the number itself as the numerator (the top number in a fraction) and 1 as the denominator (the bottom number in a fraction). So…
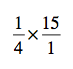
Now, here’s the multiplication rule. Just multiply the numerators together and then the denominators together.
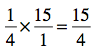
How easy is that? But what does 15/4 really mean? This is called an improper fraction — which just means that it’s got a numerator that’s bigger than the denominator. But it has a much, much bigger meaning — improper fractions are bigger than one.
How many pizzas is 15/4? Well this is easy too.
Fractions mean division. So to turn an improper fraction into divide the denominator into the numerator. But 4 doesn’t divide evenly into 15. In fact, 4 goes into 15 three times, with 3 left over. (Or as your third-grade self said: 3, with a remainder of 3.)
The whole number is the number of times 4 divides into 15. The remainder becomes the numerator of a fraction, and 4 stays in the denominator. Like this:
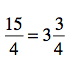
Whew! What this is means is that you need 3 and 3/4 pizzas. I don’t know of any pizzeria that delivers in this way, so round up to 4 pizzas, and you should be good to go.
That’s a lot of information. So here’s a quick summary:
1. Any whole number can be written as a fraction. Just use the number as the numerator and put a 1 in the denominator.
2. To multiply fractions, multiply the numerators together and then multiply the denominators together.
3. To change an improper fraction to a mixed number, divide the denominator into the numerator. The whole number answer is the whole number in the mixed number. The remainder is the numerator, and the denominator stays the same.
Show me (or better yet, yourself) what you’ve got with these examples. I’ll have the answers in Wednesday’s post. Questions? Ask them in the comments section.
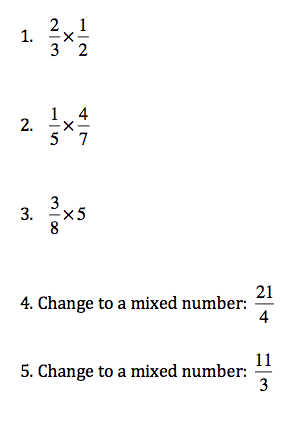
Answers to Friday’s challenge questions: -30, -2, 5, 32, -14. How did you do?







Comments are closed.