While the development of numbers continued for many, many centuries, even before the discovery or invention of zero, the Greeks were responsible for a long, long period filled with mathematical advances. By 600 B.C., a fellow named Thales of Miletus brought Babylonian mathematical discoveries to Greece, which were used to calculate distance and other measurements.
But the big player in Greece was Pythagoras. (Yes, you should recognize that name.) Born in 580 B.C. in Samos, he met old-man Thales when he was but a young lad. Perhaps Thales convinced him to travel to Egypt so that he could learn the mathematics of the Babylonians. At any rate, when Pythagoras returned from his journey, he settled in Croton (which is on the eastern coast of Italy) and this is where things get strange — at least by our modern standards.
Pythagoras established a philosophical and religious school that was made up of two societies: the akousmatikoi (hearers) and mathematikoi (learned). And while his followers look much like a cult to us, Pythagoras was in fact developing the world’s first intentional, philosophical society. Members — both men and women — were intent on living a contemplative and theoretical life, and as such divorced themselves from the culture at large, becoming completely devoted to philosophical and mathematical discovery.
But in order to do this, they had to follow a very strict set of rules, which included vegetarianism, giving up all personal possessions and absolute secrecy. And then there are the really strange orders: do not pick up something that has fallen; do not touch a white rooster; do not look in a mirror beside the light.
That’s not all. Mysticism infused almost all the Pythagoreans did, which led to some really off-the-wall mathematical ideas, like their understanding of numbers.
- Nothing exists without a center, and so the circle is considered the parent of all other shapes. It was called the monad or “The First, The Essence, The Foundation, and Unity” — or according to Pythagoras, “god and the good.”
- The dyad was a line segment and considered to be the “door between One and Many.” It was described as audacity and anguish, illustrating the tension between the monad and something even larger.
- And then there’s the triad, which of course represents the number 3. Continuing in their pseudo-anthropomorphism of numbers, the triad is considered the first born, with characteristics like wisdom, peace and harmony.
I could go on. Seriously. But while the ideas of the Pythagoreans were kind of kooky, this band of deep-thinking brothers and sisters advanced mathematics in some pretty significant ways. First of all, they began classifying numbers as even and odd, prime and composite, triangular, square, perfect and irrational. Through their strange ideas of numbers, they popularized geometric constructions. They are also attributed with the discovery of the five regular solids (tetrahedron, hexahedron, octahedron, iscosahedron and dodecahedron).
But their biggest discovery is the theorem named for Pythagoras. The Pythagorean Theorem states that the in a right triangle, the square of the longest side is equal to the sum of the squares of the remaining two sides. In other words:
This is more than just a silly formula you needed to memorize in high school. Carpenters use it to be sure that they have right angles (in other words that their door frames, decks, and walls are “square”). It’s useful to find the diagonal of a television set (which is how those contraptions are measured for some reason), if you only know its length and width. And it’s the basis of a great deal of additional math discovery, like the distance formula and various area formulas.
It’s a big, honkin’ deal. And in some ways, we’re lucky it survived the secrecy of the Pythagoreans. Pythagoras wrote nothing down. (If tin foil had been invented, he might have been wearing a hat of the stuff.) But despite its closed society, this cult of nutty mathematicians and philosophers is considered one of the most important influences in all of history.
What do you remember of Pythagoras from your high school geometry class? Have you used the Pythagorean theorem in your everyday or work life? If so, how?


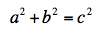






Comments are closed.