So I’ve been harping on the fact that math is flexible. And I’ve also said more than once that we do the math that we need to do. (No one here is suggesting that calculus computations are necessary for everyday life.) In fact, because of those first two facts, we often don’t need to write down literal equations at all – we might not even know we’re using a formula.
Here’s an example: Let’s say you need to build a fence around your tomato plants. If you know that the bed is 4 feet by 2 feet, how much fencing do you need? (Yes, I’m ready for spring and summer and fresh veggies. Will this cold weather ever end??)
This is a perimeter problem. Some of you might write down the formula for perimeter of a rectangle: P = 2l + 2w. But I’d be willing to bet that most of us simply add: 4 + 2 + 4 + 2 = 12 feet. No formula needed, right?
But what if we turn the problem on its head? Let say you have 12 feet of fencing, and you’re building a tomato plant bed that must be no longer than 4 feet. How wide can the bed be?
Again, there are tons and tons of ways to approach this problem. One is with literal equations. What do you know about the information you have? The perimeter and the length. What are you solving for? The width.
P = 2l + 2w
The object of the game is to solve the formula for w, in terms of P and l. (Stay with me here. I promise this is easier than that previous sentence made it sound.) To do that, you need to get w by itself on one side of the equation. This is where the algebra comes in.
The most important rule about solving algebraic equations is this: Whatever you do to one side of the equation, you must do to the other. Period. End of Sentence. Amen. Shalom. To do that, you need to undo the operations. It’s like taking something apart. Here’s how it works:
Don’t panic! This is not as messy as it looks. All you need to do now is substitute what you already know, use the order of operations to simplify, and you’ll have w.
So the width of the tomato bed must be 2 feet. My point is not that you must always solve a problem like this one in this way. Nuh-uh. My point is that there’s algebra behind this problem – no matter how you solve it. And whether you like it or not.
How would you have solved this perimeter problem? See if you can spot the algebra in your approach. And share in the comments section.
I am so pleased to be Meagan Francis‘s guest this month on The Kitchen Hour, her 45-minute podcast for parents on the go. We talk about math anxiety, math education and how to encourage our kids to embrace math — while overcoming our own fears. Listen and/or download the podcast at The Kitchen Hour.


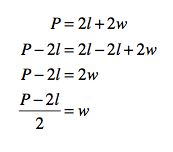
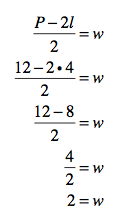





Comments are closed.