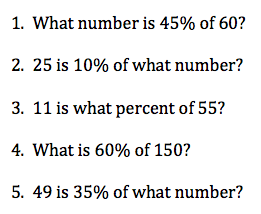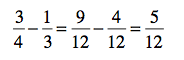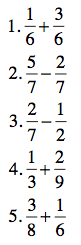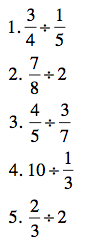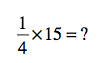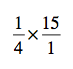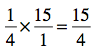Categories
Algebra Math for Grownups Math for Parents

Algebra: What good is it anyway?

Hating on algebra is all the rage these days. From New York Times editorials to cute little Facebook images, it seems that we’re settling into a big assumption: algebra is not useful to the average person. For the most part, this idea is pretty harmless. When I see those Facebook posts, I generally smile to myself and think, “Oh you’re using algebra. You just don’t know it!” (And yes, sometimes I say this out loud. I work alone, and my cats don’t care.)

But of course when there are calls to remove algebra from high school math curriculum, things get pretty serious. If you had driven past me at lunch time one fall day last year, you might have seen me (literally) shaking my fist and shouting at my radio. My local public radio station was airing a talk show featuring some doofus (I think he was a philosophy professor?) who was advocating that we actually stop teaching algebra. Seems it upsets students too much and, heck, we don’t need it anyway.

Want to make me mad? All you have to do is suggest this in a serious way.

So, prompted by all of the online ribbing that I get from people, I’ve decided to take on a challenge. This month, I’ll be writing about exactly how algebra is useful. My goal is to convince anyone who thinks differently that they’re wrong. But I know this is a tough sell. So I’ll settle for a couple of small concessions.

My thought is that I’ll focus on everyday uses for algebra (from spreadsheets to formulas), algebraic thinking (how we can think critically, thanks to algebra) and why I believe algebra is a cornerstone subject for middle and high school students.

Want to challenge my thinking? Go right ahead! Want to offer your own experience? Please do! I’d love to promote a real conversation on this topic. I can always learn something new about how real, live people use the math devoted to finding x.

In the meantime, share your algebra story in the comments section. I’d love to hear from everyone — whether algebra was the first time math clicked for you or you were one of those folks who said forget it, once letters were introduced to your math.

Categories
Math for Parents Math for Teachers

Math Summer Camps: Guest post by Lynn Salvo of MathTree

So last summer, I wrote about my disdain for math-geared summer camps. And I was summarily schooled by my friend Lynn Salvo, founder of MathTree, which offers summer camps in Virginia, Washington D.C., Maryland and Delaware. She was right, of course, and I invited her to share why a summer camp centered on math can be a rewarding experience for parents and students. Mind changed. (Thank you, Lynn.)

While summer is a great time to kick back and recharge, the down side is that kids forget a lot of math over the summer.  Studies show that during the lazy months of summer, all kids suffer from “brain drain” or the loss of learning. In fact, students lose (on average) 2.6 months of mathematical competency in June, July and August.  Only the most math-minded and determined parents can find the math in everyday life to keep math going over the summer.  A couple of weeks of a math camp anywhere in the summer can bridge the long gap.

I am president of  MathTree, which I founded in 1999 to address this very issue.  We have been providing math camps for children ages five to15 throughout the DC, Virginia, Maryland and Delaware area ever since, mostly in the summer but also during long school breaks.  Children love our camps and return summer after summer.  Some have even grown up to be instructors for us themselves.

If you’re reading this blog, you probably know math is not the most popular subject.  MathTree would have gone out of business long ago if we had not found a formula that works to provide a great summer math experience for kids.  In a typical school setting, younger children are taught math by amazing elementary school teachers who are generalists, not specialists. And unfortunately, many of them don’t really like math all that well.  Summer is a great time to give your child an opportunity to work with folks who love math, love kids, and love teaching kids math!

So what should you be looking for and how can you evaluate the math (summer) camp possibilities you are considering for your child?  Here are some questions:

  • Does the camp provide different ways of learning there is not time for in a packed school curriculum?
  • Does the camp promise an adventure?  Will the camp creatively lead my child on a mathematical exploration?  At MathTree we have our own mathical characters, including Princess KrisTen; Grouper, the Regrouper; and Numero, the Number Wizard, which we use to happily engage our campers in fun math exploration.
  • Is my child going to be set up to make mathematical discoveries?
  • Will my child play fun math-rich games?  For instance, we play games such as Ten Mingle to learn numbers that add up to 10 or Product Parfait to master multiplication facts.

Other important questions should include:

  • Will my child actively engage with people who can sense subtlety and nuance in my child’s understanding or will s/he be babysat by an electronic device?
  • Does the camp provide a sustained and focused learning experience? Does it develop momentum and go deep into math?
  • Does the camp focus on why, not just how?  Will my child learn concepts, not just processes?  For example, will my child learn what division is, not just how to do it?
  • Does the camp provide an enriching head start on the big ideas coming in math in the next school year?
  • Will my child be placed with mathematical peers or lumped with others of the same age or grade regardless of where they are mathematically? It’s critical that your child is neither frustrated (too hard) nor bored (too easy).
  • How will my child be assessed?  Will my child’s understanding be monitored in multiple ways, even in simple conversations?
  • What is the staff to camper ratio?  Your child may have suffered already in a large class.

I firmly believe that parents should always look for classes with less than 15 campers where there is a teacher and an assistant.  Here is what the teacher can do in that setting:

  • Actively engage your child in the learning
  • Tune in to your child — your child is not a number!
  • Embrace your child’s unique personality
  • Notice if your child looks confused
  • Jump in quickly and “unconfuse” your child.

Here’s what the assistant can do in that setting:

  • Handle routine tasks so the teacher can be fresh and creative with the class
  • Check children’s work quickly
  • Prepare rich math materials for children to use and store them after use so there is more quality class time
  • Provide a challenge if your child gets ahead of the group.

Whichever camp you choose, take the selection of your children’s summer math camp seriously.  You want your child to come away loving math (more) and you want to feel you got a high return on your investment.

MathTree has been growing our children’s love of math since 1999. For more information about MathTree and registration, please go to www.MathTree.com.  MathTree provides summer camps for kids in 25 locations in DC, DE, MD, and VA.  Use our camp locator to find a MathTree camp near you.

Categories
Math for Grownups Math for Teachers Math for Writers Statistics

That’s So Random: Getting sampling right

On Wednesday, we talked about sample bias, or ways to really screw up the results of a survey or study. So how can researchers avoid this problem? By being random.

There are several kinds of samples from simple random samples to convenience samples, and the type that is chosen determines the reliability of the data. The more random the selection of samples, the more reliable the results. Here’s a run down of several different types:

Simple Random Sample: The most reliable option, the simple random sample works well because each member of the population has the same chance of being selected. There are several different ways to select the sample — from a lottery to a number table to computer-generated values. The values can be replaced for a second possible selection or each selection can be held out, so that there are no duplicate selections.

Stratified Sample: In some cases it makes sense to divide the population into subgroups and then conduct a random sample of each subgroup. This method helps researchers highlight a particular subgroup in a sample, which can be useful when observing the relationship between two or more subgroups. The number of members selected from each subgroup must match that subgroup’s representation in the larger population.

What the heck does that mean? Let’s say a researcher is studying glaucoma progression and eye color. If 25% of the population has blue eyes, 25% of the sample must also. If 40% of the population has brown eyes, so must 40% of the sample. Otherwise, the conclusions may be unreliable, because the samples do not reflect the entire population.

Then there are the samples that don’t provide such reliable results:

Quota Sample: In this scenario, the researcher deliberately sets a quota for a certain strata. When done honestly, this allows for representation of minority groups of the population.  But it does mean that the sample is no longer random. For example, if you wanted to know how elementary-school teachers feel about a new dress code developed by the school district, a random sample may not include any male teachers, because there are so few of them. However, requiring that a certain number of male teachers be included in the sample insures that male teachers are represented — even though the sample is no longer random.

Purposeful Sample: When it’s difficult to identify members of a population, researchers may include any member who is available. And when those already selected for the sample recommend other members, this is called a Snowball Sample. While this type is not random, it is a way to look at more invisible issues, including sexual assault and illness.

Convenience Sample: When you’re looking for quick and dirty, a convenience sample is it. Remember when survey companies stalked folks at the mall? That’s a convenience or accidental sample. These depend on someone being at the right (wrong?) place at the right (wrong?) time. When people volunteer for a sample, that’s also a convenience sample.

So whenever you’re looking at data, consider how the sample was formed. If the results look funny, it could be because the sample was off.

On Monday, I’ll tackle sample size (something that I had hoped to include today, but didn’t get to). Meantime, if you have questions about how sampling is done, ask away!

Categories
Math for Grownups Math for Teachers Math for Writers Statistics

One in a Million: How sample bias affects data

Continuing with our review of basic math skills, let’s take a little look-see at statistics. This field is not only vast (and confusing for many folks) but also hugely important in our daily lives. Just about every single thing we do has some sort of relationship to statistics — from watching television to buying a car to supporting a political candidate to making medical decisions. Like it or not, stats rule our world. Unfortunately, trusting bad data can lead to big problems. 

First some definitions. A population is the entire group that the researchers are interested in. So, if a school system wants to know parents’ attitudes about school starting times, the population would be all parents and caregivers with children who attend school in that district.

A sample is a subset of the population. It would be nice to track the viewing habits of every single television viewer, but that’s just not a realistic endeavor. So A.C. Nielsen Co. puts its set-top boxes in a sample of homes. The trick is to be sure that this sample is big enough (more on that Friday) and that its representative.  When samples don’t represent the larger population, the results aren’t worth a darn. Here’s an example:

Ever hear of President Landon? There’s good reason for that. But on Halloween 1936, a Literary Digestpoll predicted that Gov. Alfred Landon of Kansas would defeat President Franklin Delano Roosevelt come November.

And why not? The organization had come to this conclusion based on an enormous sample, mailing out 10 million sample ballots, asking recipients how they planned to vote. In fact, about 1 in 4 Americans had been asked to participate, with stunning results: the magazine predicted that Landon would win 57.1% of the popular vote and an electoral college margin of 370 to 161. The problem? This list was created using registers of telephone numbers, club membership rosters and magazine subscription lists.

Remember, this was 1936, the height of the Great Depression and also long before telephones  and magazine subscriptions became common fixtures in most families. Literary Digest had sampled largely middle- and upper-class voters, which is not at all representative of the larger population.  At the same time, only 2.4 million people actually responded to the survey, just under 25 percent of the original sample size.

On Election day, the American public delivered a scorching defeat to Gov. Landon, who won electoral college votes in Vermont and Maine only. This was also the death knell for Literary Digest, which folded a few years later.

This example neatly describes two forms of sample bias: selection bias and nonresponse bias. Selection bias occurs when there is a flaw in the sample selection process. In order for a statistic to be trustworthy, the sample must be representative of the entire population. For example, conducting a survey of homeowners in one neighborhood cannot represent all homeowners in a city.

Self-selection can also play a role in selection bias. If a poll, survey or study depends solely on participants volunteering on their own, the sample will not necessarily be representative of the entire population. There’s a certain amount of self-selection in any survey, poll or study. But there are ways to minimize the effects of this problem.

Nonresponse bias is related to self-selection. It occurs when people choose not to respond, often because doing so is too difficult. For this reason, mailed surveys are not the best option.  In-person polling has the least risk of nonresponse bias, while telephone carries a slightly higher risk.

If you’re familiar with information technology, you know the old adage: Garbage in, garbage out. This definitely holds true for statistics. And this is precisely why Mark Twain’s characterization of number crunching — “Lies, damned lies and statistics” — is so apropos. When the sample is bad, the results will be too, but that doesn’t stop some from unintentionally or intentionally misleading the public with bad stats. If you plan to make good decisions at any point in your everyday life, well, you’d better be able to cull the lies from the good samples.

If you have questions about sample bias, please ask in the comments section. Meantime, here are the answers to last Wednesday’s practice with percentage change problems: –2%, 7%, –6%, –35%. Friday, we’ll talk about sample size, which (to me) is a magical idea. Really!

Categories
Math at Work Monday

Math at Work Monday: Lance the spirits distiller

I do enjoy a good whiskey. So when I had the chance to interview a real, live distiller, I jumped at it. Bonus: Lance Winters is funny as hell. Seriously. He’s also not shy about explaining how he uses math in his work — including his background in nuclear engineering, which has nothing to do with his current work. He is a master distiller at St. George Spirits in Alameda, CA, where he helps create artisanal spirits, including gin, absinthe, bourbon, single malt whiskey (my favorite), rum and liqueurs.

Can you explain what you do for a living?

I spend a lot of time wandering around looking busy in the hope that nobody asks me to do any actual work. When that gets too tiring, I play video games. When I do work, I crush and ferment fruit, mash in and ferment grain, then distill them. I prepare our distillates for bottling, then bottle them.

When do you use basic math in your job?  

I use math all the time! I’m not even kidding. It starts with figuring out the potential alcohol by volume in whatever medium we’re fermenting, then converting that to the total number of proof gallons we can produce from the amount of fruit or grain that we’ve had delivered. I then convert that to the number of cases of bottled product we can produce. That’s all pretty basic multiplication and division. We also use math when scaling up lab samples and bench trials of different whiskey blends.

Do you use any technology to help with this math?  

I like to use calculators to check my math and be totally sure about things, but like to do as much as possible in my head, on the fly. My memory’s bad enough that I need to keep the processor sharp.

How do you think math helps you do your job better?

I’m able to plan my work better and make more informed business decisions because of math.

How comfortable with math do you feel?  Does this math feel different to you?  

I’m very comfortable with math, all the time. I used to think that so much of math (especially calculus) was just something that mathematicians used to show off for one another. Now, I see the poetry as well as usefulness of integrals and derivatives. (By the way, I found Matt Damon very implausible as a math whiz in Good Will Hunting.)

What kind of math did you take in high school?  

I took pre-calculus in high school, and in spite of having learned at the feet of Harold Gene Smith, greatest math teacher ever, I felt like a total hack at math.

Did you have to learn new skills in order to do the math you use in your job? 

After high school, I spent two years going to navy schools to learn nuclear engineering. That totally messed my head up and made me the way I am today.

Any questions for Lance? Ask them in the comment section. I’ll let him know that they’re there, and perhaps between his daily wandering and video games, he’ll stop by to reply.

Categories
Math for Grownups Math for Teachers

Math Warriors: The comedic side of math

As I continue to crawl from under a mountain of work, I thought I’d share a really cool webseries that I discovered late last year. It’s not clear if the series will continue this spring or not, but you can take a look at the first two seasons on YouTube or the Math Warriors‘ website. 

Not since Tina Fey and Lindsay Lohan have math geeks been so cool. Math Warriors satirical look at a fictitious rivalry between Harvard’s and Yale’s math teams. And tucked away in each episode is a little bit of math. See if you can find it.

Season 1, Episode 1

Season 1, Episode 2

Season 1, Episode 3

What do you think? Stay tuned for more episodes. Or, if you can’t wait, check out the Math Warriorswebsite.

Categories
Basic Math Review Math for Grownups Math for Writers

Smaller Crowds: Calculating Percentage Change

No, I did not have the flu. No, I did not fall off the face of the earth. No, I did not abandon my math-writing career in favor of tightrope walking at the circus. In fact, I have simply been overworked. Apparently math writers are hard to find, and with the Common Core State Standards Initiative coming down the pike, I’ve had more work than I can handle. That’s a good thing — except when I can’t find time to blog or eat a nutritious meal or even get a full night’s sleep. Don’t feel sorry for me. But please don’t be mad at me for the radio silence, either. Thank you.

When last we met, percentages were the topic of discussion. I had promised to shed some light on the mysteries of percentage increase and percentage decrease. This is, by far, the most-often asked question from writers. From time to time, I’ll meet a freelancer who is trying to find the percentage decrease of a company’s profit over the previous year. Or a freelancer may want to know how to calculate the percentage increase of  her income over the previous quarter.

Trust me. This is not difficult. But it is confusing. So my challenge is to lay this out in a way that you can both understand and remember. Let’s go.

First a definition. Percentage change — which can be either an increase or a decrease — is simply a comparison of values. In this case, we’re comparing the new value to the old value and expressing that as a percent.  And here’s how you do that:

(new value – old value) ÷ old value

That’s it. But let’s break it down. The change is found by subtracting the new value from the old value. And the percentage is found by dividing that answer by the old value. In other words:

Change:new value – old value

Percentage:divide by old value

This should make sense, because change is often found by subtracting. If you pay for $15 worth of gas, using a $20 bill, your change is $5 — which is also $20 – $15. Likewise, percent means division. To find what percent 15 is of 20, you divide: 15 ÷ 20.

Let’s look at this with an example. The crowds at President Obama’s first inaugural were much, much larger than at his second. It is estimated that 1.8 million people were on the mall in 2009, while only 540,000 showed up two weeks ago. (It’s worth noting that no one can say for sure how many people attend any event on the Washington Mall. These are simply estimates, which can vary widely.) What is the percentage decrease of the crowds from 2009 to 2013?

Change: 540,000 – 1,800,000 = –1,260,000

Percentage: –1,260,000 ÷ 1,800,000 = –0.7 = –70%

So attendance at the second inaugural had decreased by 70%. (Notice that negative sign? Whenever the percentage change represents a decrease, the percentage will be negative.)

Follow the exact same process to find the percentage increase. Each year — no matter who is in office — the cost of inauguration events goes up. President Obama’s first inauguration had a price tag of $160 million. While we won’t know how much the 2013 inauguration cost for several months, we can compare 2009 to Bush’s second inauguration in 2005, which totaled $158 million. What is the percentage change from 2005 to 2009?

Change: 160,000,000 – 158,000,000 = 2,000,000

Percentage: 2,000,000 ÷ 158,000,000 = 0.01 = 1%

The cost of the inaugural increased by 1% from 2005 to 2009. (Because the answer is positive, we know the percentage change represents an increase.)

For percentage change problems, don’t worry about whether you’re finding the percentage increase or percentage decrease. The answer — negative or positive — will reveal that. Instead, focus on the two steps: 1) New number – old number; 2) Divide by old number; 3) Change the decimal to a percent.

Practice with these examples. I’ll post the answers on Friday.

Find the percentage change:

1) In 2011, a company posted profits of $305 million. In 2012, profits were $299 million.

2) When she was in the fifth grade, Sally was 54 inches tall. As a sixth grader, she’s 58 inches tall.

3) Springfield has begun a recycling program in an effort to reduce the trash collected in the city. The year before the recycling program was enacted, the city collected 160,000 tons of trash. The year after the program began, the city collected 151,000 tons of trash.

4) Since her son went off to college, Margo has noticed that her grocery bills have declined. In July, she spent $327 on groceries, while in September, she spent $213.

Questions about this process? Do you find percentage change differently? Share them in the comments section. Meanwhile, here are the answers to the last blog post’s percent problems: 27, 250, 20, 90, 140.

Categories
Basic Math Review Math for Grownups Math for Writers

Finding Percentages and the Numbers That Go With Them

So yesterday, we reviewed some really basic stuff about percentages. Like: 10% is the same thing as 1/10 or 0.1. Easy peasy, right? Well, today it’s time to really put this stuff to work, finding percentages of numbers or the numbers, given the percentages. Oy. I can hear you groaning from here.

Most folks forget when to multiply and when to divide. So I’m going to show you a process that works no matter what kind of percentage problem you’re doing. For reals. It’s why it was important for you to know about turning percentages into fractions. Let’s start with an example.

You’ve had your eye on a gorgeous cashmere sweater for months and it’s finally on sale. But can you afford it? The original price is $125, but it’s now on sale for 30% off. Do you multiply or divide or what to find out what you’d be saving with this sale?

All you need for this problem — and pretty much all other percentage problems — is to set up a proportion. What is that, you ask? A proportion is made up of two equal ratios or fractions. The proportion you need for a percentage problem is this one:

If you can remember this proportion — and how to use it — you’re home free. So let’s dissect it a bit to help you remember. The fraction (or ratio) on the right of the proportion represents the percentage itself. You should recognize this from yesterday, when you learned to change a percent to a fraction, right? So in this problem, that ratio will be 30 over 100. That’s because the sweater is 30% off.

The ratio on the left is a little tricker, but not by much. It is the percent off of the sweater over the original price of the sweater: the part of the price over the whole price. Got it? The original price (or whole price) is $125. But we don’t know the discount (or part of the price). Let’s call that x.

DON’T PANIC! That little old x isn’t going to hurt you one bit. Promise. Just because you have an x in your math problem does not make it too challenging to solve.

But yes, you will need to solve for x. This involves two, very simple steps: Cross multiply and then get x by itself. There are tons and tons of shortcuts for this kind of a problem, but for now, we’re going to stick with the more scenic route.

To cross multiply, just multiply the x by 100 and then the 125 by the 30.

100x = 125 • 30Do you have to have the equation in that order? Nope. 125 • 30 = 100x works the same way. Heck you can even multiply in any order. Now, just start simplifying and getting x by itself:

Now, remind me, what is x? Is the price of the sweater? Nope. It’s what you would save if you bought the sweater at 30% off. The sale price of the sweater is $125 – $37.5 or $87.50.

That wasn’t so painful, was it?

But what if you needed to know what percent a number was of another number? Let’s say you just had lunch with your dad, who is known for being a bit stingy. He left a $7.50 tip on a $50 check. Was it enough? Well, set up that proportion, why don’t you?

What’s the whole? $50 or the total cost of lunch. And what’s the part? That would be the tip or $7.50. You are trying to find the percent, and 100 is always 100. Substitute, cross multiply, isolate x and voila!

Looky there, good old Dad did okay with the tip — 15%.

You can also use this proportion to find the whole, when you know the percentage and the part. Just substitute what you know, shove xin there for what you want to find and follow the same darned steps as the previous examples.

Seriously ya’ll, if you can remember this one proportion, percentages will no longer be a huge stumbling block. But I can hear a couple of you whining: “What about percent increase or percent decrease???” You’ll have to wait until Friday. (Promise. It’s not all that difficult either.)

This is a good thing to practice, so try out these problems. Remember: Identify the part, whole and percent before you use the proportion. (That’s not going to be as easy with these, because they’re not word problems.) Then cross multiply and get x by itself.

Questions about this process? Do you have any better ideas? (I’ll bet you do!) Share them in the comments section. Meanwhile, here are the answers to yesterday’s percent problems: 11/20, 41/50, 3/20, 0.04, 0.31, 1.4. How did you do?

Categories
Basic Math Review Math for Grownups

Parts Is Parts: Get a handle on percents

Ever have one of those strings of bad ju-ju that just won’t quit? Welcome to the last two weeks of my life. From email woes to blog problems, it’s as if the electronic gods have cursed me. This is my way of explaining why there was no post yesterday. I’ll make it up to you today — as I wait on hold for the good folks at Comcast to answer my call about my email account. Wish me luck!

It’s the third week of our review of basic math. Time for percents. These little guys are everywhere — from the mall to your tax return to your kid’s grades to the nutritional label on your Cheerios. You simply cannot go a day without coming across a percent in one form or another.

(Try it. Just for today, notice the percents. If you’re so inclined, jot them down and post what you noticed in the comments section.)

So what’s the big deal? What are percents so darned ubiquitous?

Percents represent a part of the whole. We love to know what part of our extra-cheese, deep-dish pizza is fat or what part of the population is in favor of gun control. This information helps us make decisions and form opinions. And because of the way that percents are found, they’re not so challenging, actually.

First the basics: if you break down the word percent, you will immediately understand what it means. Per means every and (in the U.S.) a cent is 1/100 of a dollar. So percent literally means for every 1/100. Get it? (It should be noted that the notion of a percent came long before the U.S. penny, but the one-cent coin has its roots in Roman currency, which launched percents. Cool, huh?)

With this information, you can easily convert a percent to a fraction — which is a pretty darned useful thing to know. 10% is the same thing as 10 for every 1/100 or 10/100. The only thing left to do is simplify.

See what I did there? To turn a percent into a decimal, just put the percent over 100 and simplify. Works like a charm every single time.

But what about turning a percent into a decimal? That’s even easier. There are a couple of ways to look at this, but I chose 10% for a good reason. It’s the same thing as 1/10 or if you say it out-loud: “one-tenth.” And what’s another way of writing one-tenth? Put a decimal on it.

Think about what you learned in elementary school about decimals. One place to the left of the decimal point is the “tens” place. One to the right is the “tenths” place. Two places to the right is the “hundredths” place. And so on. If percents mean out of 100 or for every 1/100, really what you’re doing is thinking of place value.

10% = 0.10 = 0.1

All of this boils down to a really simple process. To change a percent to a decimal, move the decimal point two places to the right. Here are some examples:

Incredibly basic stuff, right? But it is important. We can use this information to help find the percent of a number or find the value of the whole, given the percent (which is a little bit harder). That’s up tomorrow and Friday.

Until then, how about giving these really simple problems a go?

Any of the above problems give you trouble? (Yep, I snuck in a few toughies, but I know you can do it. Just think it through.) Here are the answers to last Friday’s fraction problems: 2/3, 3/7, -3/14 (Yowza! That was a tricky one!), 5/9, 13/24.

Categories
Basic Math Review Math for Grownups

How Fractions Are Like Drinking: Adding and subtracting

We’re wrapping up a review of fractions today. If you missed Monday’s or Wednesday’s posts, be sure to look back to refresh your memory on multiplying and dividing fractions.

If you’re the product of a traditional elementary and middle school education, you likely spent many, many months (collectively) learning about adding and subtracting fractions. It is definitely one of the trickiest arithmetic skills to have, but it can also be quite useful. Now that you know how to multiply with fractions, you’re ready to unlock the secret of adding and subtracting them. And it all comes down to multiplying by the lowly, little 1.

This process is really easy — if the fractions in question have one important characteristic. Take a look:

Don’t solve the problem! Just look. What do the fractions have in common? You’re one smart cookie, so I’m sure you recognized that the denominators (the numbers on the bottom of the fractions) are the same — 5. And that’s the key in this process. Whenever you’re adding or subtracting fractions, you need to have common denominators. Then, all you need to do is add the numerators together and keep the same denominator.

If you took a few moments to run this through your brain, you probably wouldn’t have even needed to know this rule. And since we’re grownups, we can use this example: If you have 1 fifth of Jack Daniels and 2 fifths of Johnny Walker, how many fifths of alcohol do you actually have? Well, that would be 3 bottles or 3 fifths. (And believe me, while some of my high school students would have appreciated that example, I don’t think I could have gotten away with using it.)

Same thing is true for subtraction. Let’s say that the fraternity πππ (yeah, I made that up) is having a huge party. They’ve purchased 7 fifths of bourbon. But just before the gig gets started, one of the brothers knocks over the bar and breaks 3 of the fifths of bourbon bottles. How many are left? Well, that would be 4, right? Using this analogy, you can see that because the denominator was the same (5), all you needed to do was subtract the numerators (7 – 3) to get what was left (4).

And here’s where you can break even more rules. As a grownup, you can do these things in your head. If you need to add 1/8 yards of fabric to 1/8 yard of fabric, it’s pretty simple to see that you’re dealing with 2/8 yard (simplified, that’s 1/4 yard).

Yeah, things get a little trickier when you have different denominators. Let’s go back to that pizza example from Monday, shall we? Remember, we were figuring out how many pizzas to order, if we knew how much each person typically eats. Let’s say that you can eat 1/4 of a pizza, your sister can eat 1/3 and your brother can eat 1/2? In other words:

Notice something? Yep — no common denominator. So how do you get one? Well, there’s the short cut and then there’s the longer explanation. In case you’re curious, let’s talk explanation first.

You need a number that all three of these denominators will divide into evenly. That’s called a common multiple. In fact, it’s best if you have the least common multiple. (If you have a really good memory, you might remember that this is often referred to as an LCM.) So what’s the LCM of 4, 3 and 2? Turns out to be 12.

So the common denominator is 12, but do you just replace all of the denominators with a 12, adding 1/12, 1/12 and 1/12? No way, Jose. That won’t get you the right answer. What you need to do is change the numerator so that the denominator is 12. And to do that, you need to multiply by 1.

Remember 1 is the same as any fraction that has the same number in the numerator and denominator. So to change 1/4 to a fraction with 12 in the denominator, you’ll need to multiply by 3/3.

So, think ahead: what do you need to do to turn the other fractions into ones with 12 in the denominators? Multiply by 1. But which 1? You need to think about what number multiplied by the denominator will give you 12.

There’s another way to think about this, for sure. Think about the denominator you want: 12. What is one-fourth of 12? 3, right, so 1/4 is the same thing as 3/12. For some folks, that way of thinking is going to work much, much easier. But you can choose what works for you. Now we can solve the problem:

So in this case, you need a little more than one pizza. You can either ask your siblings to eat a little less (and get by on one pizza) or you can order two pizzas and put the rest in the freezer. (Personally, I’d choose the second option.)

Subtraction works the exact same way! Just find the common denominator and change the fractions. Then subtract, and finally, simplify your answer (if necessary).

Got it? If not, ask your questions in the comments section. And make sure you try out these practice problems to see how well you can really do! (Remember, no one’s grading anything, so what have you got to lose?)

If you have questions, don’t forget to ask them in the comments section. I also love to hear about different ways to approach these ideas. Don’t be afraid to tell us how you do things differently.

Here are the answers to Wednesday’s practice problems: 15/4, 7/16, 28/15, 30, 1/3.

Categories
Basic Math Review Math for Grownups Math for Parents

Halving a Recipe: Dividing with fractions

New here? You’ve stumbled upon January’s Review of Math Basics here at Math for Grownups. This week, we’re doing a quick refresher of fractions.  Monday was multiplication, so if you missed that, you might want to take a quick look before reading further. Math concepts build, you know. 

Psst! Wanna know a secret? Sure you do. So here you go: There’s a debate among math educators about whether dividing with fractions is useful at all. There. I said it. But don’t tell your kids or they might rebel.

But yes, I’m being somewhat serious here. Among math teachers who really, really think about these things — perhaps too much and I’m often in that camp — dividing with fractions is pretty much unnecessary. Okay, so you might need to divide with fractions (like when you’re halving a recipe). But while the process is stupidly simple (trust me), there are other ways to think about it that may make more sense.

[laurabooks]

Let’s take a look at that rule:

Dividing by a fraction is the same thing as multiplying by its reciprocal.

If you know what all of those words mean, you can recognize that this is pretty darned easy. But if your days in elementary school are long past, you might have forgotten what the reciprocal is. Luckily, this is no big deal. The reciprocal of a fraction is formed when you switch the numerator and denominator. In layman’s terms, you turn the fraction upside down. Like this:

It couldn’t be easier, right? So let’s put it all in context with an example.

See what we did there? We turned the second fraction over and multiplied instead of divided. This is called the “invert and multiply” process. Now, all we need to do is simplify the answer.

Notice how the 4 and 6 are both divisible by 2? Well, that means the fraction can be simplified. On a 4th-grade math test, this means your teacher wants you to do more work. In the real world, it just means that the fraction will be easier to work with or even understand. (When you see the result, you’ll know what I mean.)

Doesn’t 2/3 seem a lot easier to understand than 4/6? Think of recipes. Do you have a 1/6-cup measure in your cabinet? (I don’t.)

So let’s consider how this works (or why, if you’d rather) by considering a really basic division problem: 1 ÷ 1/2.

How many ½s fit into 1? That’s the question that division asks, right? Think about those measuring cups. If you had two ½ cup measuring cups, you would have the equivalent of 1 cup. In other words:

Make sense? Now here’s another way to look at it:

Let me summarize: 2 ½s fits into 1. In other words, 1÷ ½ is 2. And that turns out to be the same thing as multiplying by the reciprocal of ½, which is 2.

That’s a lot to take in, and you don’t have to know it by heart – or even fully understand. It just explains why this crazy rule works. And here’s another secret – there are lots of other ways to divide fractions. You can do it in your head. (It’s pretty easy to solve this problem without any arithmetic: ½ ÷ ¼. Right?) Or you could even find a common denominator (more on that Friday) and then just divide the numerators. (I’ll leave that process for you to figure out if you’re so inclined.)

The thing is, there aren’t many times in the real world that dividing by fractions is really necessary. Here’s an example to explain what I mean. Let’s say I’m cutting a recipe in half. The recipe calls for ¾ cup of sugar. How much will I actually need? Well, I can look at the question in a couple of different ways. (See which one jumps out at you.)

I would bet – and I can’t prove it – that most of you thought about the second option. That’s because you’re cutting the recipe in half, not dividing the recipe by 2.

In short, dividing by fractions is pretty darned simple, compared to other things you have been required to do in math. Too bad it doesn’t show up much in the real world, right?

Just for fun, try these problems on for size – using whatever method works for you. (No need to show your work!) Bonus points if you can simplify your answer, when necessary. (And no, there are no bonus points, because there are no points.)

The answers to Monday’s problems: ⅓, 4/35, 15/8 or 1⅞, 5¼, 9⅔. How did you do? ETA: Me? Not so good. I made a careless error with the last problem. The correct answer is 3 ⅔, which is explained by the comments below. 

Categories
Basic Math Review Math for Grownups Math for Parents

Pizza Anyone? Introducing fractions (+ multiplying)

Welcome to Week 2 of January’s Back to Math Basics — a quick review of the basic math that you need to do everyday math. Answers to last Friday’s integers questions are at the end of this post.

When kids are first learning about fractions, teachers often turn to something that all but the lactose- or gluten-intolerant can appreciate — pizza! (And I can empathize with the allergy inclined. For you, imagine a dairy-free, vegetable pie with polenta crust — yum!)

This is for very good reason: Fractions are simply parts of the whole. When you cut a pizza into 12 equal parts you are creating twelfths. To count them, you’d start at one piece and count around the pizza (or in random order, makes no diff): one-twelfth (1/12), two-twelfths (2/12), three-twelfths (3/12)… all the way to 12-twelfths (12/12) or the whole pizza (1). Half of the pizza is six-twelfths (6/12) or one-half (1/2). A fourth of the pizza is three-twelfths (3/12) or one-fourth (1/4). Get it?

(Okay, so it’s really, really hard to write a blog post about fractions. In Word, I can depend on something call MathType to write fractions, which I’ll create for examples below. But in paragraphs, this doesn’t work so well.  So please bear with me!)

It might make sense to start with addition and subtraction, but in this case, multiplication and division is the better start. (Spoiler alert: You’ll use multiplication to add and subtract. Really.) But just like with integers, multiplying and dividing fractions are really, really easy.

So let’s go back to those pizzas. Let’s say your son is having a birthday party, and he wants to serve pizza. If each kid can eat 1/4 of a pizza and there are 12 kids at the party, how many pizzas do you need to buy? (Seriously, this is not as dorky a question as it might sound. I have had to figure this out IRL.)

Are you actually multiplying two fractions here? Why, yes. Yes you are! In fact, any whole number can be written as a fraction — just use the number itself as the numerator (the top number in a fraction) and 1 as the denominator (the bottom number in a fraction). So…

Now, here’s the multiplication rule. Just multiply the numerators together and then the denominators together.

How easy is that? But what does 15/4 really mean? This is called an improper fraction — which just means that it’s got a numerator that’s bigger than the denominator. But it has a much, much bigger meaning — improper fractions are bigger than one.

How many pizzas is 15/4? Well this is easy too.

Fractions mean division. So to turn an improper fraction into divide the denominator into the numerator. But 4 doesn’t divide evenly into 15. In fact, 4 goes into 15 three times, with 3 left over. (Or as your third-grade self said: 3, with a remainder of 3.)

The whole number is the number of times 4 divides into 15. The remainder becomes the numerator of a fraction, and 4 stays in the denominator. Like this:

Whew! What this is means is that you need 3 and 3/4 pizzas. I don’t know of any pizzeria that delivers in this way, so round up to 4 pizzas, and you should be good to go.

That’s a lot of information. So here’s a quick summary:

1. Any whole number can be written as a fraction. Just use the number as the numerator and put a 1 in the denominator.

2. To multiply fractions, multiply the numerators together and then multiply the denominators together.

3. To change an improper fraction to a mixed number, divide the denominator into the numerator. The whole number answer is the whole number in the mixed number. The remainder is the numerator, and the denominator stays the same.

Show me (or better yet, yourself) what you’ve got with these examples. I’ll have the answers in Wednesday’s post. Questions? Ask them in the comments section.

Answers to Friday’s challenge questions: -30, -2, 5, 32, -14. How did you do?