Categories
Math for Grownups Math for Parents Math for Teachers Travel

How Far? Estimating metric distances

Earlier this month, I showed you how to convert currencies, when given the exchange rate. When you’re not using an online calculator, that process involves proportions, which are pretty simple to use, but do require a little figuring on paper. This same process works for any conversions, including miles to kilometers, liters to ounces, etc.

But while being exact with your money is pretty important, estimating how far you have to drive or walk is usually good enough. So instead of going into details about metric-to-traditional measurement conversions, let’s look at how you can find these distances with a little mental math. First, you’ll need to know a few facts:

1. A mile is longer than a kilometer. So, when you convert miles to kilometers, the answer  will be larger than the original amount. (mi –> km = larger answer)

2. A kilometer is shorter than a mile. So, when you convert kilometers to miles, the answer will be smaller than the original amount (km –> mi = smaller answer)

2. In fact, 1 mile equals 1.61 kilometers. And 1 kilometer equals 0.625 mile.

3. Those values are pretty darned close to 1.5 kilometers and 0.5 mile.

Remember, we’re estimating here, so you’re not looking for an exact answer. Forget what your middle school math teacher said about the precision of math. You don’t always need to getan exact answer. But there’s another fact you’ll need to consider:

4. The larger the value that you’re converting, the less precise your answer will be.

If you depend on the estimate 1 mi = 1.5 km and you’re converting 15 mi to km, your answer will be pretty close. BUT if you’re converting 1,468 mi to km, your estimate will be a lot lower than the actual answer.

Look, estimating is no big deal. In fact it’s a really, really powerful tool that can make your life much easier. You do need to know when estimation is in your best interests and when you should pull out the calculator. (See? Math really isn’t all that black and white!)

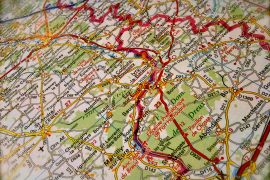
Let’s look at an example. Zoe has finally made it to London! She’s spending the summer studying Shakespeare and working part-time as a docent at the Tate Modern. And she’ll have some time to roam around Europe a bit. She’s rented a car so that she can chart her own path, and next Friday afternoon, she’s going to cross the channel to France, where she hopes to spend four days winding her way down to Paris and back.

But how long will it take her to get there? According to her map, the distance is 454 km. Since Zoe is used to miles, she’d like to convert the distance so that it makes more sense to her. She’s okay with a rough estimate, especially since she has no firm schedule. So she decides that knowing there are about 1.5 km in a mile is good enough.

To make the math even easier, she decides to round the distance as well: 450 is pretty close to 454. Now she can easily do the math in her head, but we’ll get to that in a minute. Let’s write it out first.

Because she’s converting kilometers (shorter) to miles (longer), her answer will be smaller than the original amount. That means she’ll need to divide.

450 km ÷ 1.5 = 300 mi

So she’ll travel about 300 miles to get from London to Paris — not a huge distance!

But how could she do this in her head? For that, she’ll need to remember a few things about fractions.

1.5 = 3/2

450 ÷ 1.5 = 450 ÷ 3/2

450 ÷ 3/2 = 450 • 2/3

(That’s because when you divide by a fraction, it’s the same thing as multiplying by its reciprocal — or the same fraction upside down.)

So in order to convert kilometers to miles in her head, she’ll need to multiply the value by 2 and then divide by 3 (which is the same as multiplying the value by 2/3. In other words:

450 • 2/3 = (450 • 2) ÷ 3 = 900 ÷ 3 = 300

Whew!

But once Zoe remembers this little trick, she can estimate these conversions quickly and easily.

30 km = ? mi

30 km • 2 = 60

60 ÷ 3 = 20

30 km = 20 mi (approximately)

Make sense? Try it for yourself: convert 75 km to mi and then use an online calculator to check your answer. Remember, if you’re using the process above, you’ll get an estimate, not an exact value!

So take a guess: If you’re converting mi to km, what process would you use? See if you can figure it out and then offer your explanation in the comments section. Feel free to choose a value to convert, if it’s easier to explain that way.

Categories
Basic Math Review Math for Grownups Math for Teachers

The Metric System: What’s the big deal with bases?

I’m vacationing this week in sunny Radford, Virginia,and ike most parts of the United States, the metric system is not used here (to mark distances, anyway). But if you cross the border into another part of the world, there’s little doubt that you’ll be measuring kilometers rather than miles and grams instead of pounds. That’s because most of the world has embraced the metric system. (In fact, only two other countries — Burma and Liberia — have resisted the change along with the U.S.)

Ask any scientist or mathematician: the metric system is infinitely more intuitive and much, much easier to remember and understand. But why? The answer is simple: Base 10. What this means is even simpler: in base 10 the foundational number is 10. Take a look:

10 • 1 = 10

10 • 10 = 100

10 • 100 = 1,000

and so on…

Each time you add a digit in our number system, you are effectively multiplying by 10. That means that 99 is the last two-digit number in base ten, and 999 is the last three-digit number. In fact our entire decimal system is base ten. (But it wasn’t always like that.)

But here’s the thing — you don’t care (and you shouldn’t really care). We are so used to base 10 that we don’t even think about it any more. It’s like knowing how to ride a bicycle or drive a car; once you learn it, you don’t even give it a second thought, but if you’re asked about it, it’s hard (or impossible) to explain.

When you were in school, you probably were asked to convert numbers into different base systems — and this was probably pretty darned confusing. We’re not going to do that here for one simple reason: You don’t need to know how to do this. BUT it is important to know that different base systems are useful in a variety of situations and professions. For example, computers function in base 2 (or binary), which is simply a system of zeros and ones. Computer graphics depend on a hexadecimal system or base 16 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F). Crazy, huh? Even less technical situations depend on a variety of bases — dozens and grosses are base 12 (one dozen is 1 • 12 and one gross is 12 • 12).

Compared to these other bases, base 10 is pretty darned easy, right? And that’s why so many mathy folks don’t understand why our country hasn’t embraced the metric system. Yep, unlike traditional measure systems, the metric system is base ten. Let’s compare:

Traditional system: 12 inches = 1 foot

Metric system: 100 centimeters = 1 meter

Traditional system: 5,280 feet = 1 mile

Metric system: 1,000 meters = 1 kilometers

Just a glance at these conversions and even the most math-phobic person would probably agree: the metric system is much easier to maneuver.

But agreeing that the metric system is easier doesn’t help you with conversions when you’re traveling, does it? On Wednesday, we’ll take a look at those conversions. I’ll show you some really easy ways to estimate the conversions. Because who wants to do math on vacation?

What other bases can you think of? How do you use them in your everyday life? Share your ideas in the comments section.

Categories
Math for Parents Math for Teachers Travel

Kids in the Car: Keep ’em busy with math

Whether you’re flying across country or crammed in the mini-van for a trip to Grandma’s house, keeping a kid occupied on a long trip may mean you need a vacation at the end of it. And sure, we can plug them into movies or iPods or video games, but is that really what you want your children to remember about their trip to the Grand Canyon?

Being trapped in a car or plane or train for hours at a time will either kill you or make you stronger, and I’m rooting for stronger. You can look at this as an opportunity to hang out with your kids — and even sneak in a little math.

I know that sounds really, really geeky, but this was a real, live question that a parent asked me over at MSN.com’s Mom’s Homeroom where I’m the resident math expert. Since we’re talking travel this month, I thought I’d expand on the ideas here. The parent asked: “What are some fun math games that I can play with my 10 year old son and 7 year old daughter while on road trips?”

First and Last

This is a take on a game that I used to play with my daughter. She would say a letter, and I would say a word that began with that letter. Then she would identify the last letter of that word, and give me a word that began with that letter. For example: S prompted me to say spaghetti. She would say I and then igloo.

This can easily be adapted to math, which helps kids (and adults) practice their mental computation skills. For example:

First player: 16 + 3

Second player: 19

Second player: 19 – 10

First player: 9

First player: 9 • 3

and so on…

Set the rules of the game so that everyone can play. For example, no negative numbers, fractions or exponents, if your 13 year old is playing with his 8-year-old brother. Or tell them that they can only use even numbers or only addition and division. You might just find that your kids are getting really creative — and making some cool connections. (Did you know that when you add or subtract only even numbers, the answers will always be even?)

Road Sign Math

If you’re in the car, sometimes the only thing to read are road signs and license plates. But if you take a close look, you could find some math in there. In fact, someone has created a cool wiki devoted to this game. Take a look at the sign below.

Photo courtesy of Road Sign Math wiki

Do you see the math in there? It’s a very simple addition problem: 2 + 4 = 6.

These can get downright complex! But you can keep it easy for your younger kids. Look out for route numbers, license plates and billboards for more ideas. If you’re used to traveling the same road over and over, this is a particularly good way to pass the time. What’s old becomes new again!

I Spy

This perennial favorite can be adapted to all sorts of situations. For example:

“I spy with my little eye: a prime number!”

“I spy with my little eye: 17!”

I spy with my little eye: a fraction!”

Try this with a boring magazine on the plane. Keep the questions on grade level and offer encouragement for good — or close or creative — answers. Need to remember what a prime number is? If you’re not driving, do a quick search on your smart phone.

There are countless other ideas that can help you pass the time and inject a little math into the trip. Do you have suggestions? Offer them in the comments section!

Categories
Math for Grownups Math for Teachers Travel

Keeping Current: Using proportions to convert currency

Last Friday, we looked at exchanging currency — how far will your money go in another country? In that post, I introduced you to online currency conversion calculators and helped you assess whether or not your answer made sense. Today, we’re going to look at doing these conversions by hand.

Out of every basic math skill I know and have taught, proportions are the most useful — and most often forgotten. You can use them to shrink photos proportionally (so that the Eiffel Tower doesn’t look squat and fat or that mime doesn’t resemble a human hericot vert), alter a recipe to feed an army or find unit price. With proportions, you don’t need to remember whether to multiply or divide. Get the numbers in the right place, cross multiply, solve for x, and you’re good to go.

But let’s back up for a second. What is a proportion? It’s simple, really. A proportion is merely two equivalent ratios. (Remember, a ratio is a way to compare two numbers, often written as a fraction.)

1/2= 2/4

The two fractions (ratios) in the above statement are equivalent: 1 out of 2 is the same thing as 2 out of 4. But that’s just an example. The key to setting up currency exchange proportions is knowing where each part goes.

There are four parts: the original currency ($1USD, for example), the currency exchange rate (the value of $1USD in the other currency), the value you are converting, and the value after the conversion (the answer or x). You want to be sure that all of your parts are in the right place.

But there is more than one right place! So, I suggest being consistent with these parts. That way, you can always, always use the same proportion for each conversion that you do.

($1USD)/(euro exchange rate) = (USD value)/(euro value)

That looks a little clunky, but it’s not really difficult to dissect. Look at it carefully, and you’ll notice a few things:

  1. The $USD amounts are in the numerators of the ratios.
  2. The € amounts are in the denominators of the ratios.
  3. The conversion exchange ($1USD to €) is in the first ratio, while the actual values are in the second ratio.

To use this proportion, you need three of the four values found in this proportion. What do you think they will be? One of them will always be 1, because it’s the base value of the currency exchange. If you’re converting $USD to €, you’ll use $1USD. If you’re converting € to $USD, you’ll use 1€. The second known value will be the currency rate. Last Friday, we used $1USD = 0.794921€, so let’s stick with that, making the second value 0.794921. The third value will always be the value you’re converting.

Let’s look at an example. You spy a gorgeous pair of boots in Paris for only 324€. You have $500USD budgeted for a special splurge. Are these special boots within your budget? Plug things into the proportion to see:

1/0.794921 = x/324

Before you let your nerves get the best of you, look at this proportion carefully. Which values have gone where? Now, do you think there is another way to set up this proportion? (Psst… the answer is yes.)

0.794921/1 = 324/x

Or even:

1/x = 0.794921/324

Notice that while the numbers themselves have changed places, their relative positions have not. The $USD values (1 and x) are still related (either in the same ratio or in the numerator or denominator), and the € values (0.794921 and 324) are still related (either in the same ratio of in the numerator or denominator).

But how do you solve this proportion? (In other words, “Holy crap! There’s an x in there, and it freaks me out!”) Take a deep breath and cross multiply. Choose one of the proportions above (I’m going with the first one), and picture a giant X on top of it. One segment of the X lies on top of the numerator of the first ratio and the denominator of the second ratio (the 1 and the 324). The other segment of the X lies on top of the denominator of the first ratio and the numerator of the second ratio (the 0.794921 and the x). Multiply the connected values, like this:

1 • 324 = x • 0.794921

Now you can simplify and solve for x.

324 = 0.794921x

Divide each side of the equation by 0.794921 (in order to get the x by itself).

324 ÷ 0.794921 = x

407.587672 = x

You’ve just discovered that 324€ is equal to $407.59USD. That’s within your budget, so you’re good to go!

Now, try the other conversions to show that they work, too. See? Flexibility in math! (Who knew?)

What did you think of this process? Scary? Easy? Too hard? Stupid, because you can always use a calculator? Do you have another way to convert currency (besides proportions and using a calculator)? Share your ideas in the comments section.

Categories
Math at Work Monday

Math at Work Monday: Julie the travel agent

The details involved in a big vacation can be so overwhelming. And from determining the best prices on airfare to figuring out when you’re going to arrive at your destination, there’s a ton of math involved. That’s exactly why my family contacted Julie Sturgeon, owner of Curing Cold Feet, to help us plan our trip to the Galapagos Islands several years ago. Julie is just the person you want — detail oriented, always on the lookout for the best deal and very, very careful with your hard-earned cash. She proclaims a distinct fear of math, but she’s managed to turn that around and build a very successful travel agency. She was also kind enough to bare her math soul today.

Can you explain what you do for a living? I research, recommend, and book travel packages for both family vacations and business trips. This involves checking everything from airline schedules and prices to comparing amenities for the price at all-inclusive resorts, cruise lines, and hosted tour packages. I also book hotel rooms and car rentals.

When do you use basic math in your job?  Most of my math involves basic adding, subtracting and determining percentages. For instance, if a family wants to go to Walt Disney World for 5 days, but they know nothing more than that, I would prepare charts that show the costs of a value hotel with Hopper passes versus a moderate hotel with Hopper passes versus a deluxe hotel without Hopper passes. The chart would also show what happens to the price if you add any of the three meal plans to this vacation package. This way, families can weigh their values against their budget — at $3,200, for example, would they really need a sit-down meal every day versus a fast food option at their original budget of $2,400? Or should they keep the higher food plan and stay at a less expensive hotel?

Other times, I need to show vacationers why one package is better than another. For instance, a property may be running national commercials on all the cable channels advertising “30% off your stay in July.”  A couple wants to take advantage of that deal and calls asking for it specifically. Meanwhile, a supplier has a bulk inventory pricing on the property next door, which actually has higher ratings at Trip Advisor, and that total price comes out $100 less. And the property down the beach always offers rooms at the rate from the nationally advertised brand. I need to be able to explain in simple numbers why the 30% off deal isn’t really a sale in this circumstance, so they aren’t overly impressed with something that is, in fact, ordinary.

The second way I use math is more behind the scenes. Vacation packages require a deposit, with a final payment on a specified date. Just making sure you don’t over- or underpay requires a calculator. And sometimes it can become even more complicated when two people are sharing a room and want to divide the cost into two equal payments across two credit cards. I really have to stay on the numbers ball if they choose to make incremental payments before the final payment on split credit cards!

Do you use any technology to help with this math? I use a calculator as an insurance policy that the numbers come out right. Whenever I need to translate foreign currency quotes to US dollars, I use xe.com, and I use worldtimeserver.com when determining the time difference between two countries.

How do you think math helps you do your job better? It allows me to be an advisor and research assistant as opposed to a salesperson. I am more comfortable — and therefore more effective — in that role.

How comfortable with math do you feel? I am very math phobic. When I was a journalist, I had my engineering husband check any statistics conclusions I had to make, because I didn’t trust myself to choose the right formula to get the right answer. We have a pool table, and everyone in my family tells me the key to winning a game is to use geometric principles. I’ve never won a game. At one point in my life, I thought about getting an MBA but learned I’d need to take the GMAT for my admission application. So I decided to take math lessons, borrowed a seventh grader’s textbook and ended up in tears because I couldn’t understand it. Needless to say, I’ve never taken the GMAT, and I consider an MBA closed to me.

But this feels completely different because it’s about someone’s money. This counting makes sense to me, it feels important, and it really doesn’t stray that far from the basics I learned in grade school.

What kind of math did you take in high school? I was required to take two years of math to graduate, and I enrolled in algebra and geometry. I was allowed to take classes with the word “remedial” in them for the diploma, but my pride wouldn’t let me, since I was in the accelerated track for every other topic. I passed both math classes with a C, although I had to have a tutor to get me to that point, and I spent every in-class study period getting one-on-one help from the math teacher.

Did you have to learn new skills in order to do the math you use in your job? I had everything I needed except confidence. That came only when my desire to protect people’s hard-earned money was greater than my fear.

All you need to get comfortable with basic math is a victory. It gets easier from there. Start with balancing your checkbook. Or figuring out how much faster you will be out of debt if you pay X amount more each month on a financial commitment. The fact that it’s worth real money to you is a powerful motivation, and when you get it right, you know you can do it again.

Questions for Julie? Post them in the comments section, and I’ll be sure to let her know they’re here!

Categories
Math for Grownups Math for Teachers Travel

Keeping Current: Converting currency right

You’ve booked that trip to Paris. Vive les vacances! Now that your credit card has borne the brunt of your plane tickets and hotel reservations, with just enough space for a couple of fantastic meals, it’s time to turn to the cash. How much should you bring — and even more importantly, how far will it go?

When traveling out of country, you need to consider the currency exchange rate. Only very rarely is this exchange equal. (In other words, one Euro almost never equals one U.S. dollar.) That means, you’ll need to use a conversion to find out how far your cash will actually go.

There are actually three things to talk about here: using an online conversion calculator, doing the conversions by hand and checking your answer to see if it’s reasonable. Remember, math is infinitely flexible, so there’s no reason you have to do this in one particular way. Next Wednesday, we’ll look at doing conversions with paper and pencil. Today, it’s all about online calculators and checking your answer.

First, the conversion calculators. Go ahead and use them! If nothing else, a reliable online calculator will give you the most up-to-date conversion rate with the click of a button. For example, using the XE currency conversion calculator, I found that $1USD is equal to 0.794921€ (as of Monday, July 2, 2:05 p.m.).  This means that one U.S. dollar is worth a little more than 75 percent of a Euro.

If you know the exchange rate, it’s really easy to exchange values of 10, 100 or 1000. In these cases, you can simply move the decimal point.

$10USD = 7.94921€

$100USD = 79.4921€

$1000USD = 794.921€

Notice that when there is one zero (as in 10), you move the decimal point one place to the right. When there are two zeros (as in 100), you move the decimal point two places to the right. And when there are three zeros (as in 1000), you move the decimal point three places to the right.

Of course, if you want to convert $237.50USD to Euros, that trick won’t work. In that case, you can plug $237.50 into the online calculator. If you have $237.50USD in your pocket, that’s 188.717€.

XE also has iPhone and Droid apps, so you can take the online calculator on the road with you. (Note: I don’t have any relationship with XE. It just looks like a good, reliable online currency calculator. Want to recommend something different? Feel free to respond in the comments section.)

The thing about online calculators is that they’re only as good as the information that you put in. If you think you’re converting $USD to €, but you’re actually doing it the other way around, well, your fancy pants calculator is not going to spit out the answer you were looking for. You have to know how to assess whether your answer is correct.

I’m the first to admit that I get this very confused. I have to stop and think really hard to be sure that I’ve done the conversions correctly. (And to be honest, this is one of the reasons I prefer to do it by hand.) But there are some simple rules you can consider that will help:

  • If the conversion rate is less than 1, the conversion will be less than the original amount.
  • If the conversion rate is greater than 1, the conversion will be greater than the original amount.

Let’s say that $1USD equals $1.26SGD (Singapore dollar). If you convert $USD to $SGD, will your answer be greater or less than the original amount? If you said greater — you’re right! But if you convert $SGD to $USD, the answer will be less than the original amount. Make sense?

The good news is that you can figure this out before you leave. Write it down or keep a note on your phone. Then you will always be able to check to see if your answer makes sense. Because the worst thing is to come home from a relaxing vacation to find that you’ve spent way too much.

Be sure to come back next Wednesday to get the deets on how to do these conversions by hand. It really isn’t that difficult — and the process is applicable in so many other situations, so it’s worth learning.

Where are you traveling this summer? Share your plans in the comments section below!

Categories
Math for Grownups Math for Teachers

Where’s the Dollar? An answer to Monday’s riddle

On Monday, I posted the following travel- and math-related riddle. I’m guessing everyone was too scared to post their answers — or perhaps you’re all celebrating Independence Day a little early — because no one chimed in. But no worries, my feelings aren’t hurt in the least. Still, I promised the answer, so here it is.

First the riddle itself:

Three friends are traveling to their high school reunion together. They arrive at their hotel late at night, only to find that their reservations were lost.  There is only one room with three beds available. They have no choice but to share the room, which the hotel has discounted to $30. Each of them takes out a 10 dollar bill, which the clerk collects.

After the friends are settled into their room, the manager reconsiders the discount. (He feels terrible!) He decides to offer the room at only $25 and sends a porter upstairs with $5 for the three friends.

The porter starts thinking about how to divide the $5 into three equal parts. When he can’t figure it out, he decides to give $1 to each friend, and pocket the rest. The friends accept the $3 refund, and the porter heads back to his post, with the remaining $2.

Given their $3 refund, each of the three friends paid $9 for the room (3 • 9 = $27). The porter has $2 in his pocket, making the total $29 ($27 + $2 = $29). But the friends originally paid $30!

What happened to the $1?

If you’ve been around the block a few times, you’ve probably heard this riddle. And if you google “missing dollar riddle,” you’ll find thousands of results that outline where that dollar actually is. (Heck, there’s a Wikipedia entry about it!) Most of these talk about a logical fallacy, which is a perfectly reasonable way to describe things. In my mathy brain, there’s another way to explain it, using equations.

This is what we know:

In other words, the friends originally paid $30, but the manager decided to discount the room by $5. That meant that the clerk took $25 from the original $30 and the porter took $5 from the original $30.

$30 = $25 + $5

Then the $5 was split up — $3 for the friends and $2 that the porter pocketed.

$30 = $25 + $3 + $2

Clearly there is no missing $1. Here’s another equation to prove why. If you subtract $3 from each side of the equation, you get this:

$27 = $25 + $2

This works, because with their discount of $1, each friend paid $9 for the room, rather than the original $10. Another way to look at it is this:3 • $9 = $25 (the cost of the room) + $2 (the amount the porter pocketed)$27 = $25 + $2Get it? If not, take another look. It is confusing at first, but once you see it, it does make sense.Now if you subtract the $2 from both sides of the equation, you can see how the amount that the friends paid minus the amount that the porter pocketed equals the cost of the room itself.$27 – $2 = $25$25 = $25Make sense? Sometimes it does to me, and then my understanding floats away! But I do think it can be fun to look at these problems mathematically. I hope you did, too.Did you come up with the correct reasoning before reading this? Did you use math? If not, how would you explain that the dollar is not missing at all? Share your ideas in the comments section!

Categories
Holidays Math for Grownups Math for Parents

Ah, Ohh! Math and fireworks

Here in the states, today is Independence Day — the 236 anniversary of the signing of the Declaration of Independence. (Yes, I subtracted 1776 from 2012.)

Most of us are taking the day off, but there is one industry that is working overtime: the guys and gals who choreograph and conduct fireworks displays. These gorgeous displays are patriotic, fantastical and downright dangerous.

As you can imagine, there’s a ton of math that goes on to make sure that no one in the 500,000-person crowd at the National Mall in Washington, D.C. aren’t injured by the 66,000 pounds of explosives that go off in a 20-minute show. (Oh, and for any of you math teachers out there reading, this is how to get pyrotechnic teens interested in algebra. When they ask when they would ever use conic sections or quadratic equations, talk to them about fireworks and Punkin chunkin.)

[laurabooks]

So we’re not going to get into the nitty-gritty of the math here. Instead, let’s look at the concepts behind the math involved. First, you need to know how fireworks are set off.  The shell is set in a mortar tube, which rests on the ground. When the fuse is lit, a chemical reaction forces the shell into the air, following a predictable path.

As long as everything is timed and spaced properly, the shell bursts and the debris begins to fall back to the ground. You can replicate this (safely) with a tennis ball. Throw it up in the air and watch what happens.

You’ll notice that the ball rises and, once it hits a certain height, starts to fall again. If you throw it straight up, it will go higher. If you throw it at an angle, it goes farther out. (Parents: This is a really cool experiment for kids. Have them try throwing the ball at a number of different angles.

What happens? Estimate the angle at which you’re throwing the ball. (Straight up and down is 90 degrees.) Then measure the distance from where you threw the ball and where it landed. What kinds of connections can you make between the two?) This is called a trajectory. Physics dictates that the path an object takes when launched into the air will be a curve. Specifically, this curve is a parabola.

The water in this water fountain forms a parabola. (Photo courtesy of Paul Anderson)

Here’s the math part: Every curve has an equation associated with it. That equation describes all sorts of things — like how tall and wide the curve is. But why do fireworks geeks care? Because the equation keeps everyone safe. The firework must be launched at the correct angle, or it could land in the middle of the watching crowd. This magic number depends on the firework in question. Heavier explosives must have greater force behind them. They need that velocity to get them to the right height. Second math part: These equations are always quadratic. In other words, their highest exponent is 2, like this:

x2 + 3x – 9 = 0

For most of the population, solving this equation isn’t important. But I do think it can be useful to know a few things:

  1.  Linear equations don’t have exponents,
  2.  Curves have exponents, and
  3.  Quadratic equations represent parabolas.

Of course, anyone who is interested in getting into the fireworks biz is going to have to know more than that.

So there you have it. A tiny fraction of the math behind fireworks. Now you have even more to ooh and ahh about.

Questions about fireworks or quadratic equations? Ask them in the comments section! I’ll track down the answers for you if I can. (I’m no chemist or physicist, though!)

Categories
Math for Grownups Travel

Get Out the Map: July is for traveling

Welcome to July! School is officially out, and temperatures have risen. This is the month when many folks decide to hit the road.

Whether you’re RVing across country, boarding a plane for a distant land or just heading down to the beach for some R&R, you’ll need to pack some math skills. From budgeting your costs to figuring out exactly when you’ll arrive, a vacation is no time to rest your brain cells completely. Math can help you save some cash, stay on time and even avoid a nasty sunburn.

This month, we’ll look at all of the ins and outs of travel math. We’ll hear from travel agents and other pros who play a role in your vacation plans. I’ll share some ways that math can keep you on track. Heck, we can even take a look at your odds in Vegas. (I promise, no trains leaving from two different stations at the same time — unless you need to that a problem like that solved for you.)

If you have ideas for a post, do drop me a line. In the meantime, I’ll leave you with this logic problem:

Three friends are traveling to their high school reunion together. They arrive at their hotel late at night, only to find that their reservations were lost.  There is only one room with three beds available. They have no choice but to share the room, which the hotel has discounted to $30. Each of them takes out a 10 dollar bill, which the clerk collects.

After the friends are settled into their room, the manager reconsiders the discount. (He feels terrible!) He decides to offer the room at only $25 and sends a porter upstairs with $5 for the three friends.

The porter starts thinking about how to divide the $5 into three equal parts. When he can’t figure it out, he decides to give $1 to each friend, and pocket the rest. The friends accept the $3 refund, and the porter heads back to his post, with the remaining $2.

Given their $3 refund, each of the three friends paid $9 for the room (3 • 9 = $27). The porter has $2 in his pocket, making the total $29 ($27 + $2 = $29). But the friends originally paid $30!

What happened to the $1?

Think you know the answer? Share it in the comments section. Then come back on Wednesday to see if you’re right!

Where is the $1? Post your answer in the comments section. Also, feel free to share your vacation math questions. I’ll address as many as I can throughout the month of July!

Categories
Health Math for Grownups Math for Parents

Feeling the Burn: The math of SPF

It’s the last post of June, but we have a lot more summer to go. That means a lot more opportunities to enjoy the outdoors — and expose ourselves to damaging UV rays. Not only is a burn uncomfortable (or downright painful), but it comes with a whole host of other problems, from wrinkles to cancer. Take a look at these facts from the Skin Cancer Foundation:

  • More than 3.5 million skin cancers in over two million people are diagnosed annually. That’s more than the combined incidence of cancers of the breast, prostate, lung and colon.
  • One in five Americans will develop skin cancer in the course of a lifetime.
  • Over the past 31 years, more people have had skin cancer than all other cancers combined.
  • Between 40 and 50 percent of Americans who live to age 65 will have skin cancer at least once.
  • One person dies of melanoma every 62 minutes.
  • One or more blistering sunburns in childhood or adolescence more than double a person’s chances of developing melanoma later in life.
  • A person’s risk for melanoma doubles if he or she has had more than five sunburns at any age.

So that’s a lot of numbers and statistics. (Believe me, I only shared a fraction of what I found.) But there are other really important numbers to consider: SPF or sun protection factor.

Basically, SPF is the estimate of time that you can be in the sun without burning. This is really easy math. Let’s assume that without sunscreen, you would burn after 15 minutes. If you used a sunscreen with SPF 15, you’d be able to stay in the sun 15 times as long without burning:

15 minutes • 15 = 225 minutes

225 minutes ÷ 60 = 3.75 hours

If you used a sunscreen with SPF 30, you be able to stay out twice as long:

15 minutes • 30 = 450 minutes

450 minutes ÷ 60 = 7.5 hours

But can you add SPF values? In other words, if you put on SPF 15 and then SPF 30, would you have SPF 45? Mathematically speaking, yes. But in actuality, nope. You’re only as good as the highest SPF you applied.

It’s also important to note that SPF ratings are averages. So while these calculations can help protect you from a nasty burn, you can’t count on them for down-to-the-minute protection. (There’s that imprecision-of-math thing again.)

There are also many, many other variables to consider — including time of day (sun exposure is harshest between 10:00 a.m. and 2:00 p.m.), location (water and sand reflect light, intensifying the rays) and activity levels (sweat and water can cause sunscreen to wear off).

The bottom line? You can do all of the calculating you want, but the only sure-fire way to prevent a sunburn — and the health risks associated with it — is to avoid the sun. Protective clothing can help, along with staying out of the sun when it’s at its strongest. And look for new labeling on sunscreen products. Last summer, the Food and Drug Administration (FDA) introduced new rules for these products, which will start showing up next summer.

This is perhaps the most basic math of all, so there’s no need to make it complicated. For once, you don’t need to multiply or do figures in your head. Just follow these simple rules:

1. Wear the highest reasonable SPF levels. (The FDA says SPF 50 is the best you can do.)

2. Everyone needs sunscreen. All skin types can burn or at least suffer from skin damage. So even if you have dark skin, apply sunscreen.

3. Cover up as much as possible, with broad hats, swim shirts and umbrellas.

4. Avoid the sun at peak times, especially if you plan to be on the water or beach.

5. Reapply sunscreen at least every two hours, more often if you’re sweating or getting in and out of the water.

Simple, eh?

How do you manage the sun and outdoor activities in the summer? If you have cool tips to share, post them in the comments section!

On Monday, we’ll take off on a month of travel math. Got questions? Let me know, and I’ll track down the answers.

Categories
Home Math for Grownups Math for Teachers

The Mighty Hexagon: Let bees help you garden

On Monday, Cristina Santiestevan of Outlaw Garden shared a post about the geometry of gardening, introducing us to the idea of “hexagonal spacing.” This was such a cool idea that I thought I’d explore it further. I wanted to know the math behind it. In other words, why are hexagons so darned special?

Let’s start by with the bees. In research for a magazine assignment, I’ve done some reading about bees lately, and once again, I’m in absolute awe. These little guys are the linchpins of our ecosystem in a lot of ways. Not only does their pollen-collecting insure the reproduction of a variety of plant species (and therefore the survival of critters that depend on these plants), but their colonies are efficient little factories that seem to mirror human manufacturing — from the dance the workers do to relay directions to the best pollen to the efficiency of their job descriptions.

And then there are the hives. If you think of the bees as efficient — and they are — you can deign why the hive is made up of tiny hexagons. (Remember, a hexagon is a six-sided figure.) Not wanting to waste any space whatsoever, the bees figured it out: instead of making circular cells, which leave gaps around the sides, they create a tessellation of hexagons, which leave no empty space at all.

Photo courtesy of wildxplorer

(A tessellation is the repetition of a geometric shape with no space between the figures. Think M.C. Escher or a tile floor.)

The same concept applies to gardening. Why waste space? As Cristina pointed out, choosing a hexagon-shaped planting scheme, you’ll get more plants in your beds.  And if you’ve got an outlaw garden, like Cristina, it’s best to make the most of your space! Here’s how:

In regular rows, you plant 6″ apart in only two directions, getting nice, even rows. But if you consider six directions, you’re replicating the hexagon, instead of a square — and as a result maximizing your space (just like the honey bees). Cristina describes it as planting on the diagonal. Or you can think of each plant at the center of the hexagon.  Then you can plant the others 6″ from the center in six directions — creating the vertices of the hexagon. (If you’ve ever looked carefully at a Grandmother’s Flower Garden quilt pattern, this idea might jump out at you. Not only is each plant the center of a hexagon, but it’s also the vertex of another hexagon.)

Drawing courtesy of Cristina Santiesteven

Did you see what I did there? Math can be described in a variety of ways! Look at the second diagram carefully, and see what jumps out at you — the hexagons or the diagonal rows?

So there you have it. We can learn a lot from a bee. And I can already think of times when this can be useful in other areas. How many more cookies can you fit on a cookie sheet, if you arrange them diagonally (or in a hexagon shape) rather than horizontal rows? What about kids desks in a classroom?

Where can you apply the hexagon to make your space more efficient? Share your ideas in the comments section!

Categories
Home Math for Grownups Math for Parents

Garden Geometry: A guest post from the Outlaw Garden

My thumb isn’t even remotely green. The only plants I have any success with are those that can sustain a tremendous amount of neglect — like hydrangea, hostas and lariope. So I asked fellow write and founder of Outlaw Garden, Cristina Santiestevan to step in with some gardening math. She does not under-deliver! Check out the mad geometry skills she has. Then put her tips to work in your own garden. 

In the garden, math is everywhere. There’s arithmetic and subtraction, which gardeners use to estimate how long it will take for a tomato to ripen or a seed to sprout. There’s multiplication, which helps gardeners calculate expected yields. And, there’s higher math too. Lots and lots of higher math.

Yesterday, for example, I used a measuring tape and a bit of high school geometry to confirm that my tomato trellis would be a nice (right-angled) rectangle, rather than a slightly askew parallelogram. I also used an online calculator, because figuring out the square root of 10,116 isn’t especially easy to do by hand. I knew I’d get a number close to 100, but I wanted to be sure.

Turns out that the square root of 10,116 is 100.57832768544127. I rounded to 100.5, because my measuring tape isn’t quite that fine-tuned.

If you haven’t guessed yet, I was using the Pythagorean Theorem: a2 + b2 = c2. As an avid DIYer, I use this formula a lot. It’s a great way to be sure that your project will be square, with four right angles. That’s essential if you’re building any sort of box, especially if you’ll be adding a door later. A slight skew away from 90° can create all sorts of trouble.

In this case, the motivation is all aesthetics. This trellis could work fine as a parallelogram. The tomatoes wouldn’t even notice. But, I would.

So, here’s how I did it. The trellis is 96 inches tall and 30 inches wide. Those are our a and b sides. Putting them into the equation, we get 962 + 302 = c2. That works out to

9216 + 900 = c2

10,116 = c2

This is when I googled “square root,” in hopes of finding an online square root calculator. I knew it would come in close to 100, because 100 • 100 = 10,000. But, I wanted to be as exact as possible. That’s where the online calculator came in handy. The answer — 100.57832768544127 — was more precise than I really needed. 100.5 inches is plenty good enough when building trellises in the garden.

With that number in mind, I measured the diagonal from top to bottom on both sides of the trellis. One side measured about 100.25 inches and the other measured about 100.75 inches. A slight adjustment, and both sides measured 100.5 inches. The trellis was square. Success!

Here’s the plan for the trellis. You can see where the right triangle would go:

(Cristina has a great post detailing the step-by-step process for building her trellis, including a downloadable pdf of her plans. Check it out here.)

Trellises aren’t the only place we use and see geometry in the garden. The Pythagorean Theorem is a great help to gardeners who want to ensure their garden beds and paths are perfect squares or rectangles, for example. And, equilateral triangles — three equal sides — provide guidance when planting the garden. While most books tell us to plant our vegetables in rows that are square to each other, that’s not the best way to maximize our garden space. No. Instead, plant your rows on a diagonal, using an equilateral triangle as your guide, and you will be able to fit more plants into the same amount of space. Like this:

See how a series of six triangles creates a hexagon in the diagonal planting pattern? That’s where the extra space efficiency comes in; you’re basically planting on a hexagonal pattern. And, as bees already know, the hexagon is the most efficient shape.

Even plants have geometry. All members of the mint family have perfectly square stems, like this bee balm:

Sedges — a grass-like bog plant — have triangular stems. Some plants, like dogwood and maple trees, follow a perfect symmetry with their leaves. These are known as opposite plants, because their leaves form opposite one another on their branches. Alternate plants, on the other hand, form their leaves singularly or in groups, on alternate sides of the branch. Other plants grow their leaves and flowers in whorls or rosettes:

The dogwood has opposite leaves.

Virginia Sweetspire has alternate leaves.

The leaves of the culversroot are in a rosette pattern.

And, the Fibonacci Sequence is everywhere:

The pattern of the yellow spirals in this chamomile are based on the Fibonacci sequence

Thank you, Cristina! My advice to you, dear reader: do not miss her blog, Outlaw Garden; it’s funny, informative and really, really clever. Do you spend time in the garden? What kind of math do you use and see while tending your plants? If you have questions, don’t hesitate to ask in the comments section. Don’t worry, I’ll ask Cristina to come by to respond. (It’ll be better that way.)